Algorithms and Data Structures for Programming Contests

Graph Traversal Algorithms

Discussion

What is this about?

• Graphs G = (V,E):
  • Vertex (or node) set V = {v₁,...,v_n}.
  • Edge (or arc) set E = {e₁,...,e_m}, where e_j = (u,v) for u,v ∈ V.
  • Directed graph: (u,v) ≠ (v,u), self-loops (v,v) allowed, e.g.,

    

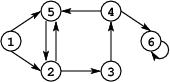
  • Undirected graph: (u,v) = (v,u), self-loops disallowed, e.g.,

    

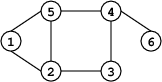
• Terminology: u is neighbour of v if (v,u) ∈ E — note: different from (u,v) ∈ E.
• Traversal algorithm: systematic way to "visit" each vertex in G.
  Two standard traversals: depth-first search (DFS), breadth-first search (BFS).

Depth-first search

• Given graph G = (V,E) and first node to visit.
• Initialization:
  1. Mark each node "undiscovered".
  2. Push first node onto empty stack.
• While stack not empty:
  1. Remove top node v from stack.
  2. If v is "discovered", go back to start of loop.
  3. Mark v "discovered".
  4. Visit v (application-specific).
  5. Push all undiscovered neighbours of v onto stack.

Breadth-first search

• Given graph G = (V,E) and first node to visit.
• Initialization:
  1. Mark each node "undiscovered".
  2. Append first node to empty queue.
• While queue not empty:
  1. Remove front node v from queue.
  2. If v is "discovered", go back to start of loop.
  3. Mark v "discovered".
  4. Visit v (application-specific).
  5. Append all undiscovered neighbours of v to queue.

Try it! (1)

• Try the "Portals Redux" problem from the DWITE programming contest.
• Ignore issues of input/output for now: suppose you already have the data stored in an appropriate data structure of your choice.

Regroup

© Copyright 2012–2015 François Pitt <francois.pitt@utoronto.ca>
last updated at 08:25 (EST) on Thu 5 Mar 2015
Algorithms and Data Structures by François Pitt is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.