CSC 324 2006W
ASSIGNMENT 2

1. Define sum so that one can write code similar to the mathematical summation notation :

       (sum i = 1 to 10 (* i i)) => 385

   Here = and to are keywords, i is a single user-supplied variable, (* i i) is a single user-supplied expression, 1 and 10 are user-supplied expressions that evaluate to integers. If the first integer is larger than the second, the result of sum should be zero (this matches the mathematical convention). The integers should be evaluated at most once during execution, to avoid problems if they come from expressions with side-effects.

2. Define free that takes an expression e composed of lambda expressions, and returns a list representing the set of all variables that occur free in e. The list must not contain multiple copies of variables. For example,

   (free '((lambda (x) (x y (z))) (lambda (a) (lambda (n) ((a n) (c z))))))  => (y z c)

   All symbols except lambda should be considered variables, and you may assume the expression does not contain any macros or other syntactic forms (in particular, it does not include let, if, quote, quasiquote, etc.).

3. The cond expression in Scheme chooses one set of expressions to evaluate depending on which test returns true. The switch statement in C permits flow to ``fall through'' to the next clause unless a break statement appears. We combine these ideas in this question.

   Define cond* which takes several clauses (much like the Scheme cond), where each clause starts with a test (or the keyword else), contains one or more expressions, and optionally ends with the keyword break.

   When evaluated, each clause is considered in order left-to-right. The test is evaluated and:

   • If the test evaluates to #f, the clause is skipped and the next clause is considered.
   • If the test does not evaluate to #f, the rest of the expressions within the clause are evaluated in order. If the clause ends with break, the value of the preceding expression is returned. If the clause does not end with break, flow ``falls through'' to the next clause: the test is evaluated (and value is ignored) and the following expressions are evaluated. This continues until a break is encountered as the final expression in a clause, or there are no clauses remaining in the cond*, in which case the value of the last expression is returned.

   Once a clause is matched, no further clauses are considered for matching. If the keyword else appears instead of a test, the clause is automatically matched.

   For example, the following two expressions are equivalent and both return 2:

   (cond* (#t 1 2 break)                        (cond (#t 1 2)
          (#f 3 4 break))                             (#f 3 4))

   The following expression would evaluate the first test (#t), evaluate 1 and 2, and ``fall through'' to the next clause. The test would be evaluated (#f) and result discarded, followed by evaluating 3 and 4. This is the end of the cond* expression, so 4 would be returned.

   (cond* (#t 1 2)
          (#f 3 4))

4. Propositional calculus (or sentential logic) contains constants true and false, a set of propositional variables, four binary connectives (and, or, implies, iff) and one unary operator (not). We will model well-formed formulas of propositional calculus as follows:
   • Any symbol, #t or #f is a wff.
   • If 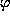is a wff, then (not 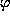) is a wff.
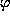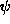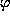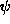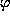   • If and are wffs, then ( and ), ( or 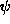), ( 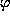implies 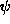), ( 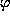iff 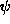) are wffs.
   • Nothing else is a wff.

   Notice that wffs are fully parenthesized for this question.

   1. Define proposition-wff? that takes a single argument and returns whether it is a well-formed formula.
   2. Define proposition-eval that takes a wff and a list of variables, and returns the truth value of the wff when those variables are true and any others are false.
   3. Define proposition-satisfiable? that takes a wff and returns whether some setting of its variables makes the proposition true.
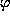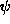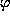   4. Define proposition-normalize that takes a wff and returns an equivalent wff where all negations are moved as far inside as possible, using the usual rules of propositional calculus (for ( iff ) use the negated form ( iff (not ))).

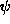5. 1. Consider the following class-like procedure:

        (define (Circular-Queue capacity)
          (let ((v (make-vector capacity))
                (head 0)
                (size 0))
            (lambda args
              (let ((m (car args)))
                (cond ((equal? m 'size) size)
                      ((equal? m 'enqueue)
                       (vector-set! v (modulo (+ head size) capacity) (cadr args))
                       (set! size (+ size 1)))
                      ((equal? m 'dequeue)
                       (set! size (- size 1))
                       (let ((r (vector-ref v head)))
                         (set! head (modulo (+ head 1) capacity))
                         r)))))))

      Rewrite it so that each branch of cond produces a procedure, and apply the (result of) cond to the cdr of args.

   2. Write a syntactic form class so that one can write the above as:

        (define Circular-Queue
          (class (capacity)
            ; list of pairs of instance variable and initial value
            ((v (make-vector capacity))
             (head 0)
             (size 0))
            ; pairs of method header and body
            ((size) size)
            ((enqueue o)
             (vector-set! v (modulo (+ head size) capacity) o)
             (set! size (+ size 1)))
            ((dequeue)
             (set! size (- size 1))
             (let ((r (vector-ref v head)))
               (set! head (modulo (+ head 1) capacity))
               r))))

      Don't worry about handling methods that take an arbitrary number of arguments.

   3. Rewrite class so that the instance variables are in two lists, according to whether we automatically want getter methods created:

        (define Circular-Queue
          (class (capacity)
            (private
               (v (make-vector capacity))
               (head 0))
            (public
               (size 0)
               (capacity capacity)) ; let's make capacity public as well
            ((enqueue o)
             (vector-set! v (modulo (+ head size) capacity) o)
             (set! size (+ size 1)))
            ((dequeue)
             (set! size (- size 1))
             (let ((r (vector-ref v head)))
               (set! head (modulo (+ head 1) capacity))
               r))))

      Each instance variable list is optional, but you may assume that they appear before the methods, and if both appear then private appears before public.

      Notice we are getting the benefits of the Java getter method convention for instance variable access, without having to write those methods ourselves!

      HINT: Use more than one rule, and have some of them rewrite into the other forms.

   4. Extend class from (b) to allow getter variables to be annotated where they are declared:

        (define Circular-Queue
          (class (capacity)
            ((capacity get capacity)
             (v (make-vector capacity))
             (head 0)
             (size get 0))
            ((enqueue o)
             (vector-set! v (modulo (+ head size) capacity) o)
             (set! size (+ size 1)))
            ((dequeue)
             (set! size (- size 1))
             (let ((r (vector-ref v head)))
               (set! head (modulo (+ head 1) capacity))
               r))))

      You may allow the explict lists from (c) after the non-explicit one.

      HINT: Use rules that recursively rewrite this into (almost) the explict form of (c).

   5. In this part we'll add subclassing to (d).

      Because of the way that syntax-rules works, we can't introduce a meaning for this or super into class and give it meaning to the user of class. Most serious Scheme implementations provide more powerful macro systems that handle this, but for simplicity we'll just require the user to specify the name used to refer to the superclass part of the object. What this means in the implementation is simply that super should not be treated as a keyword. What this means for the user is that they aren't restricted to using the name super.

      Extend class from (d) so that it handles an optional call to a superclass in the form shown below:

        (define Point
          (class (x y)
            ((x get x)
             (y get y))
            ((equal? p) (and (= x (p 'x)) (= y (p 'y))))))
      
        (define Coloured-Point
          (class (colour x y) (super (Point x y))
            ((colour get colour)
            ((equal? p) (and (super 'equal? p) (equal? colour (p 'colour)))))))

      HINT: Add a private instance variable for the superclass object. Add a catch-all procedure to the end of the method-selecting cond that passes the method call to the superclass object. If no superclass object is specified, supply a dummy one that returns 'no-such-method regardless of the method name and arguments.