Confidentiality
Send encrypted messages across the wire.
just decrypt m' and read.
m->E (m)---------------------->m' D (m')
e d
Alice --------+-----+---------- Bob
| |
| |
| Mallory (malicious attacker)
|
Eve (eavesdropper)
Note: Keys must be secret! This is private key cryptography.
Data Integrity
Remember, we want to ensure that data has not changed since I stored it on disk. In terms of the
Alica/Bob model, we want to defend against Mallory. The best we can do is to 'ensure'
that, if Bob recieves a message, then Bob can determine that it was
created with Alices encryption key and not subsequently altered.
Alice sends m as well as Ee(m) to Bob. Bob verifies that
the message m1 recieved and the encrypted version m2 satisfy Dd(m2)=m1.
If these match then Bob has confidence that the message recieved was encrypted
using Alices private key e. Note: It is still possible for Mallory
to resend a pair previously seen. This technique protects against Mallory
manipulating the message m parts of a message.
m----------------------->m1 Check that
m->E (m)---------------------->m2 D (m2)=m1
e d
Alice --------+-----+---------- Bob
| |
| |
| Mallory (malicious attacker)
|
Eve (eavesdropper)
In what follows, we will see that instead of sending both m and E
e(m) we will send
m and hash(m).
Note: We will use a keyed hash function.
Hash Functions and their properties
You might ask, why does Alice need to send m as well as E
e(m)? That was just the setup
for hash functions. A hash function is a one way function from larger finite strings to typically smaller,
fixed length strings. To be a cryptographic hash function, there are a few properties
we would like to have.
For an unkeyed hash function h, we would like to have
- preimage resistance: given y, it is computationally difficult to find x such that h(x)=y.
- 2nd-preimage resistance: given x, it is computationally difficult to find x1 such that h(x)=h(x1).
- collision resistence: it is computationally difficult to find x0 and x1 such that h(x0)=h(x1).
Example
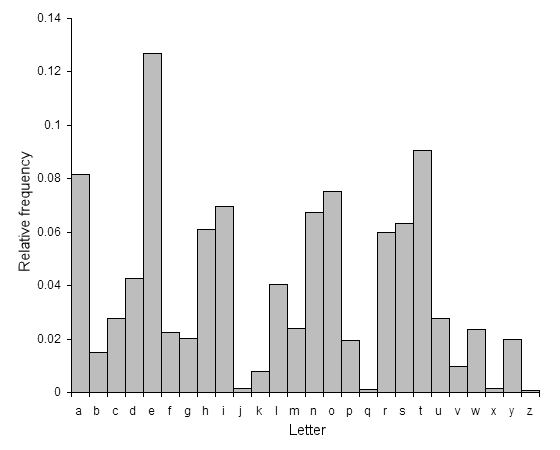
f(b b b b b ... b )=b +b +b +b +b ... +b
1 2 3 4 5 n 1 2 3 4 5 n
where + here is exclusive OR
In this example, f maps arbitrary bit strings to a single bit {0,1}.
Note: In this example, there are no keys.
Exercise:
Which of the above 3 properties does this hash function violate (it is not
a good choice for a cryptographic hash function).
Example
MD5 takes an arbitrary
string and returns 128bits (usually written as 32 hex digits).
MD5 has been broken by using Rainbow tables (rainbow report).
The idea: let MD5k be MD5 run on itself, k times. So MD53("this is something")=
MD5(MD5(MD5("this is something"))). Create a table as follows...
(intuition only, details are not necessarily correct, in fact reduce(MD5(x)) is computed in each round)...
seeds | targets
--------+----------------
| 10000
seed1 | MD5 (seed1)
|
| 10000
seed2 | MD5 (seed2)
|
| 10000
seed3 | MD5 (seed3)
. | .
. | .
. | .
| 10000
seedM | MD5 (seedM)
This is the rainbow table. We include enough entries so that every MD5 image is covered. That is,
if MD5(x)=y there is some seed in the table and a k in 1<=k<=10000 such that
MD5
k(seed)=y. You can think of each row of the table as capturing a chain
MD5(seed), MD5(MD5(seed)), MD5(MD5(MD5(seed))), ..., MD5
10000(seed).
To use this table, say I want to find a pre-image of y, do the following
let t=y
while(t is not a target in the rainbow table){
t=MD5(t)
}
we now know a chain that y appears in
assume t is in the row with seedp
last=seedp
y'=MD5(seedp)
while(true){
if(y'==y){
return last
} else {
last=y'
y'=MD5(y')
}
}
Note: If I use a larger number (>10,000) then the rainbow table becomes smaller. Each
row covers a potentially longer chain. The question is, how does one go about computing the
table in the first place. This has already been done and has to be done only one time.
We have left out the issue of whether there actually is a cryptographically secure hash function.
None has yet been proven secure (whatever that means).
Application of Hash functions to Data Integrity
Say I want to distribute software. I want to have a main distribution site as well
as mirrors. I want to ensure to be able to ensure that downloaders of my software from
mirrors will be confident that they have good, unmolested copies of my software. What do I do?
I keep a MD5 hash of my file a the main distribution site. Those interested in the software
can download it from any of the mirrors and verify their download by computing the MD5 hash of
the download and comparing it with the MD5 fingerprint downloaded from the main site.
file.zip
file.zip.md5=MD5(file.zip) -----+
MAIN |
|
+----&gt; file.zip.md5
check whether file.zip.md5=MD5(file.zip (from MIRROR4))
file.zip
MIRROR1 +----------&gt; file.zip (from MIRROR4)
|
|
file.zip |
MIRROR2 |
|
|
file.zip |
MIRROR3 |
|
|
file.zip -----------------+
MIRROR4
Note: For this to work, we need 2nd preimage resistence. Why?
Data Integrity (continued)
We left off with the question of how Alice convinces Bob that the data has arrived in tact.
Alice and Bob have a secret key k (salt possibly). Instead of using a simple hash function,
they used a keyed hash function (for example MD5(salt+message)). To ensure data integrity,
Alice sends Bob the pair (m,h(k,m)). Bob receives (m',h') and checks whether h(k,m')=h'.
Note:This does not prevent Mallory from replaying a past message. It prevents
Mallory from manipulating the message.
m-----------------------&gt;m'
h(k,m)----------------------&gt;h' Bob now verifies h'=h(k,m')
Alice --------+-----+---------- Bob
has secret | | has secret key k
key k | |
| Mallory (malicious attacker)
|
Eve (eavesdropper)
In terms of MD5, Alice and Bob would have the same secret string (called salt).
Alice would send m as well as MD5(salt+m) (+ is string concatenation).
Bob receives m' and h' and checks whether MD5(salt+m')=h'.
Authentication
Alice wants to convince Bob that Alice is on the other end of the line. Alternatively,
you want to login to your computer. First attempt:
E ('Im Alice'))------------&gt;m' Bob checks D (m')='Im Alice'
e d
Alice --------+-----+---------- Bob
| |
| |
| Mallory (malicious attacker)
|
Eve (eavesdropper)
While Bob is fairly certain that no one else could have encrypted the message 'Im Alice',
Mallory could replay the authentication. An alternative...challenge/responce. Bob chooses a
random number, sends it to Alice, Alice encrypts the random number and returns it.
Each round gives Bob more confidence that the individual on the other end of the line
is capable of encrypting using key e. Remember, Bob has key d and Alice has key e.
choose a random number x1
send it to Alice
&lt;-------------------x1
encrypt and return
E (x1) --------------------&gt;m' Bob checksD (m')=x1
e d
choose a random number x2
send it to Alice
&lt;-------------------x1
encrypt and return
E (x2) --------------------&gt;m'' Bob checksD (m'')=x2
e d
.
.
.
Alice --------+-----+---------- Bob
| |
| |
| Mallory (malicious attacker)
|
Eve (eavesdropper)
Example
Authentication in unix and /etc/shadow, /etc/passwd
As you already know, /etc/passwd is world readable. Passwords are no longer
stored there. They are instead hashed into /etc/shadow (root readable, not world readable).
In many systems, they are hashed into /etc/shadow using MD5. In light of the preimage
vulnerability (via Rainbow Tables), how can we use MD5?
When a users password is created, random salt (for this users password) is computed.
MD5(salt+password) is computed
and both the salt and MD5(salt+password) are stored in the /etc/shadow file.
When a user attempts a logs in, their entry in /etc/shadow is fetched (if it exists).
The random salt appears in that entry and this is added to the supplied password.
This is compared with the entry in /etc/shadow and, if they match, the user is
allowed to log in.
Below is a few lines taken from /etc/shadow. $1$ indicates that MD5 is used.
For arnold the salt used is $1$BrsaVm9R$. The result of salting
and MD5ing arnolds password is pAmsCoQfoijNt6H/DuRjF0. hacker's salt
is $1$ufns7sR1$.
arnold:$1$BrsaVm9R$pAmsCoQfoijNt6H/DuRjF0:14178:0:99999:7:::
hacker:$1$ufns7sR1$ryQ4O4JmtrPjzJ/X2eLp01:14178:0:99999:7:::
The following PHP script actually verifies arnold...given the password and the salt,
it produces the above hash.
&lt;?php
echo crypt('stfftatvotse','$1$BrsaVm9R$');
?&gt;
In terms of Rainbow tables, this means that to crack a particular
password (knowing the salt and MD5(salt+password)) you would actually
need to create a rainbow table specifically for this one password. You could
not use an existing rainbow table.
Exercise: How does adding salt prevent a hacker from authenticating even though they have stolen
the /etc/shadow file?