Lecture 10: Formal Language Theory 2

2025-06-04

Review

Formal languages

  • An alphabet, \(\Sigma\) is a non-empty, finite, set of symbols.
  • A string \(w\) over an alphabet \(\Sigma\) is a finite (0 or more) sequence of symbols from \(\Sigma\).
  • The set of all strings is denoted \(\Sigma^*\).
  • A language is any subset of \(\Sigma^*\).

For any language \(A\), we have the problem of determining whether a given input is in \(A\) or not.

DFAs

Deterministic Finite Automata

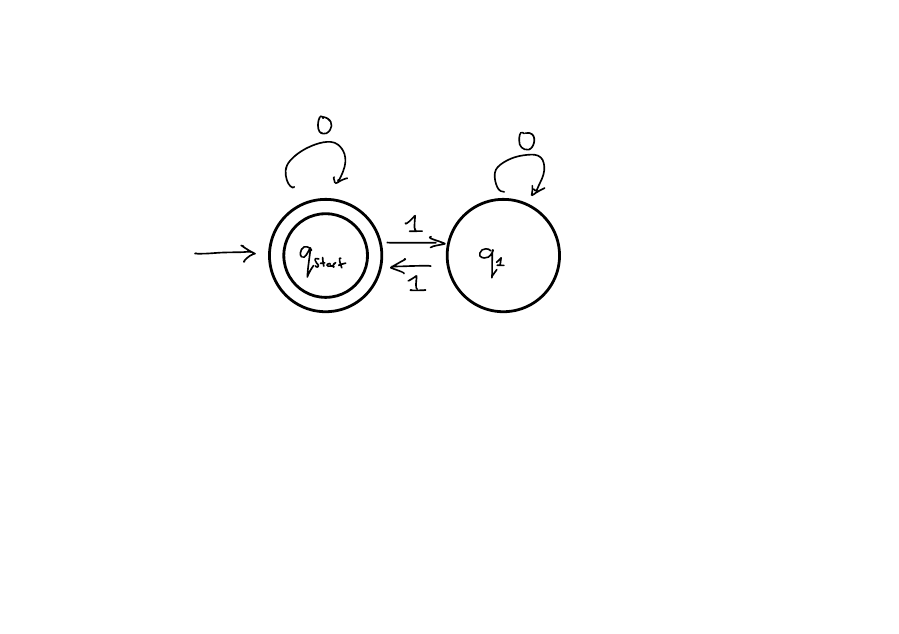
Computation:

  • Start at the start state.
  • Read each character in the input string, one at a time and follow the arrows.
  • After reading the entire string, if you are in an accept state, accept. Otherwise, reject.

NFAs

Non-deterministic Finite Automata

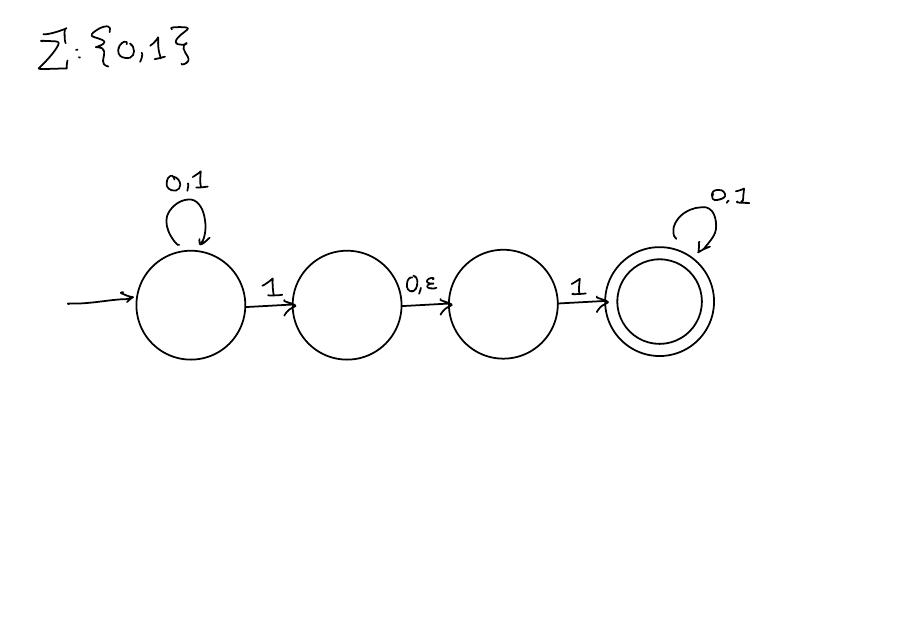
Computation:

  • Same as a DFA except now you get to choose which arrow to take if there are multiple arrows with the same character.
  • You can also choose to take an \(\epsilon\)-transition without reading a character.
  • If any sequence of choices leads to an accept state, accept.
  • Reject only if every sequence of choices leads to reject.

Regular Languages

Regular Languages

A language \(A\) is regular if and only if there is a DFA \(M\) such that \(L(M) = A\).

Closure

Suppose \(A\) and \(B\) are regular languages, then

  • \(\overline{A}\),

  • \(AB\),

  • \(A \cup B\),

  • \(A \cap B\),

  • \(A^n\), and

  • \(A^*\)

are also regular.

Let’s prove this!

\(\overline{A}\)

Suppose \(A\) is regular. Let \(M\) be a DFA for \(A\). Let \(M'\) be the DFA with all the states of \(M\) flipped. Then \(L(M') = \overline A\).

\(A \cup B\)

Let \(M\) and \(N\) be DFAs for \(A\) and \(B\) respectively. We need to find a DFA \(D\) for \(A \cup B\).

Idea 1: Here’s what we’d like to do. Let \(w\) be the input. \(D\) runs \(M\) on \(w\) to check if \(w \in A\) and then \(D\) runs \(N\) on \(w\) to check if \(w \in B\). Accept if either was accept and reject if both were rejected.

Why does this idea not work?

Solution we only get to read the input once!

\(A \cup B\)

Idea 2: Instead, we need to run the two machines in parallel. Thus, each state in \(D\) corresponds to a 2-tuple where the first element is the ‘M’ state and the second element is the ‘N’ state.

If we’re at state \((x, y)\) and we read a character \(\sigma\). Then we transition to \((x', y')\) where \(x'\) is the state that \(x\) goes to (in \(M\)) when reading \(\sigma\) and \(y'\) is the state that \(y\) goes to (in \(N\)) when reading \(\sigma\).

What should the accepting states be? \((x, y)\) should be accepting if either \(x\) was an accept state in \(M\) or \(y\) was an accept state in \(N\) (or both).

Example: Starts with \(1\) or has an even number of 1s

Solution 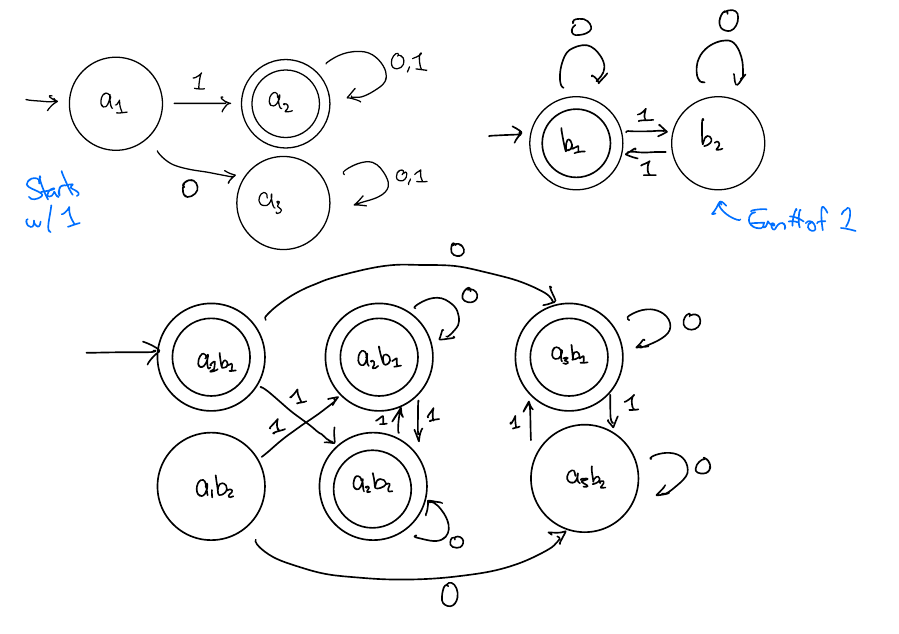Note some states are never reached here (and can be removed)

\(A \cap B\)

Homework.

Review

  • DFAs

  • A language \(A\) is regular iff there is a DFA \(M\) such that \(L(M)=A\)

Closure

Suppose \(A\) and \(B\) are regular languages, then

  • \(\overline{A}\) (by flipping states),

  • \(A \cup B\) (by running two DFAs in parallel),

  • \(A \cap B\) (hw),

  • \(AB\) (today!),

  • \(A^n\)(today!), and

  • \(A^*\)(today!),

are also regular.

\(AB\)

The same trick of running the DFAs in parallel doesn’t work.

How would you write code to solve this?
Solution

On input \(w\):

  • For \(i = 0,1,...,n:\)

    • inA = \(M(w[:i])\)

    • inB = \(M(w[i:])\)

    • if inA and inB: accept

  • reject

The idea is to try all the different ways to split up the string, if there is a way to split the string up such that the first half is in \(A\) and the second half is in \(B\), then accept. If no way to split up the string works, reject.

Review: Nondeterminism

“If any sequence of choices leads to an accept state, accept”

“Reject only if every sequence of choices leads to reject”

Choices

  • If there are multiple arrows marked with the read character, choose which arrow to take.

  • If there is an \(\epsilon\)-transition, choose whether or not to take it!

Equivalence

Equivalence of DFAs and NFAs

Let \(A\) be any language. There is a DFA \(M\) such that \(A = L(M)\) if and only if there exists a NFA \(N\) such that \(A = L(N)\).

The forward direction is true since every DFA is already a NFA (it just doesn’t use the extra features). The backwards direction might be surprising to you!

Essentially it says all the extra features we give NFAs don’t in fact give them more “power”. If I can solve it with an NFA, I can also solve it with a DFA.

NFA \(\implies\) DFA

We need to simulate a NFA \(N\) with a DFA \(M\)

High level idea:

  • Have a state in \(M\) for every subset of states in \(N\).

  • Let \(S\), \(T\) be two states in \(M\). Then \(S\) transitions to \(T\) reading \(\sigma\) if some choice allows me to go from a state in \(S\) to a state in \(T\). The choice includes an unlimited number of \(\epsilon\) transitions.

  • The accepts states are the subsets that contain accept states.

  • The start state is the subset containing the start state in \(N\) and all states reachable from the start state using an \(\epsilon\) transition

Intuitively, if I’m at state \(S\) after having read \(w\). \(S\) should contain all the possible states I could have been in \(N\).

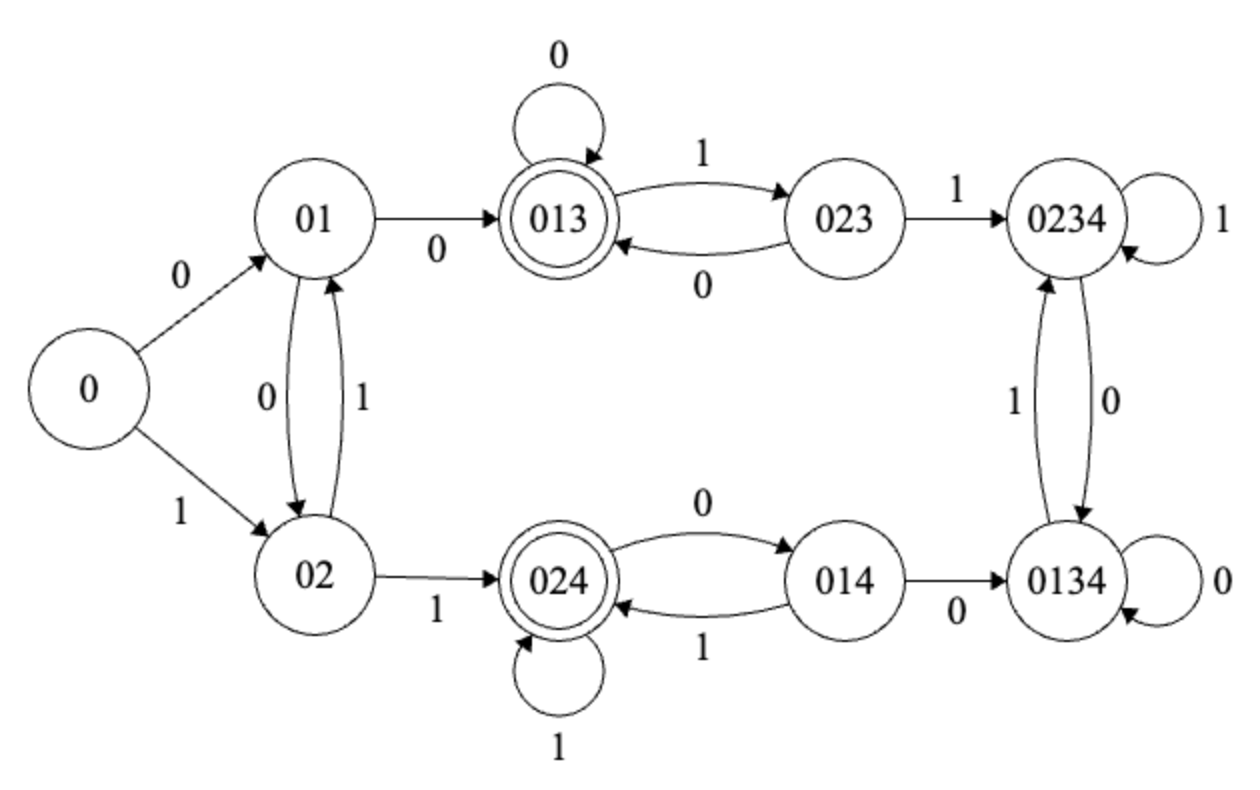
Example

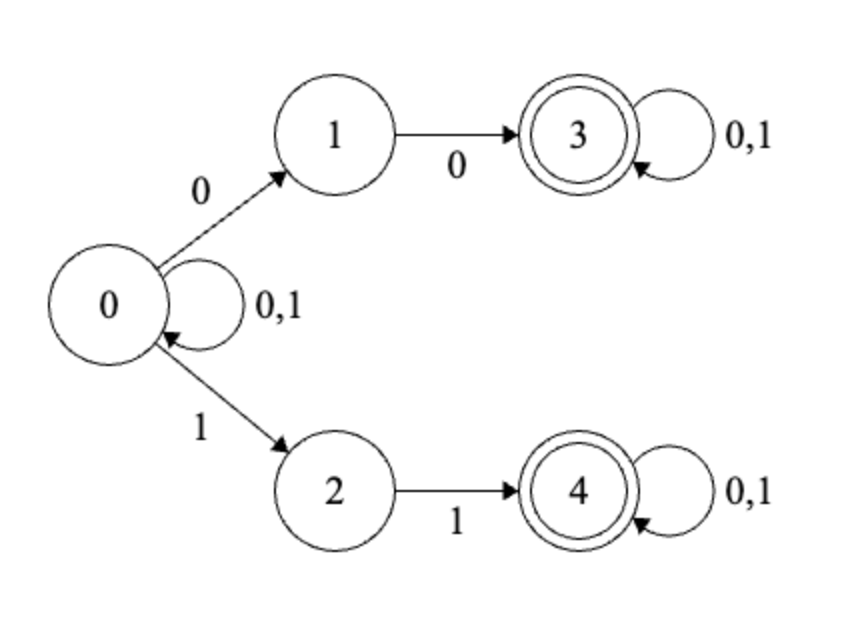
Solution

Takeaway

For every NFA \(N\), there exists a (potentially huge) DFA \(M\) such that \(L(N) = L(M)\).

Regular Languages (again)

The following are equivalent

  • \(A\) is regular

  • There is a DFA \(M\) such that \(L(M) = A\)

  • There is a NFA \(N\) such that \(L(N) = A\)

Equivalent models of computation

The more complex a model of computation, the easier it is to use. I.e. NFAs are more complex so finding NFAs for a language is easier than finding DFAs for language.

The more limited a model of computation, the easier it is to prove things about. Since DFAs are so restrictive, we can prove a lot of nice properties about them!

Since these two models of computation are equivalent, we can pick the right model for the right situation!

\(AB\) is regular

Solution

Let \(M\) and \(N\) be DFAs for \(A\) and \(B\) respectively. We’ll show that \(AB\) is regular by finding an NFA \(H\) for \(AB\).

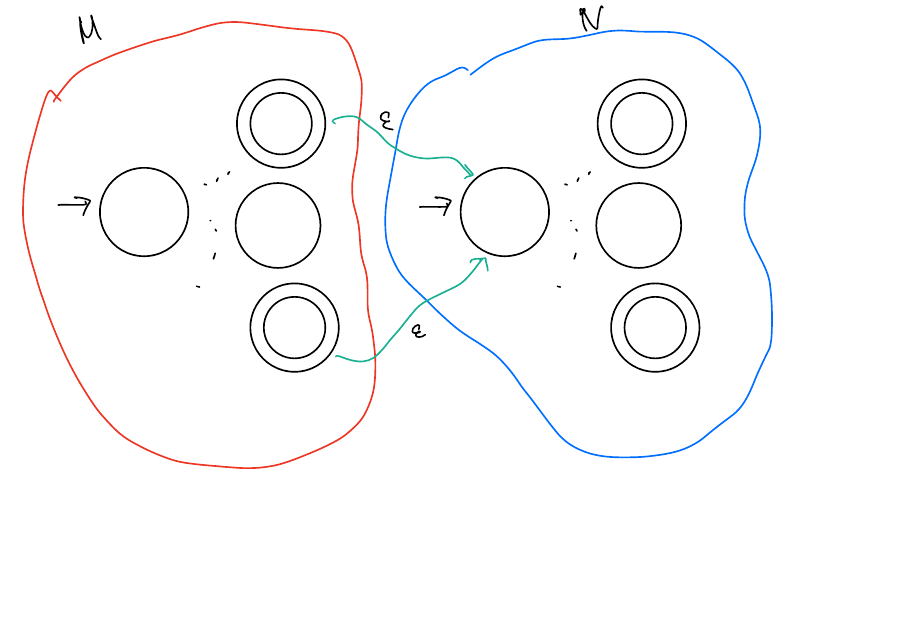
\(AB\)

This NFA guesses when the string in \(B\) should start. It starts in \(M\) and can only move to \(N\) from accepts states in \(M\) since we need the first part of the string to be part of \(A\).

\(A^n\)

Suppose \(A\) was regular, how would you show that \(\forall n \in \mathbb{N}. A^n\) is regular?

Solution By induction!

\(A^*\)

Solution

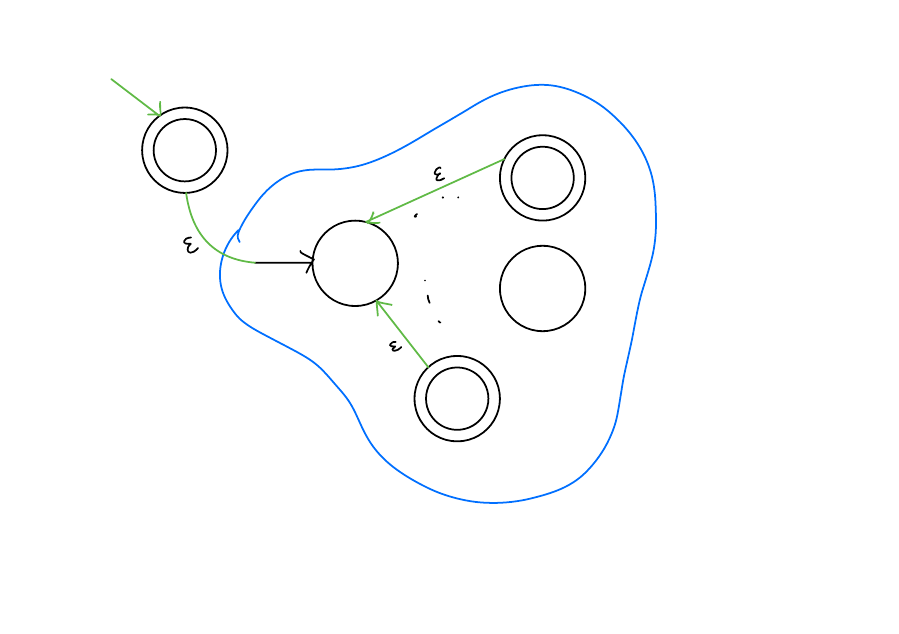
Regex

Regular Expressions

Regular expressions are all about matching patterns in strings.

Examples:

Regular Expressions - Formally

Let \(\Sigma\) be an alphabet. Define the set of regular expressions \(\mathcal{R}_\Sigma\) recursively as follows.

\(\mathcal{R}_\Sigma\) is the smallest set such that

  • \(\emptyset \in \mathcal{R}_\Sigma\)

  • \(\epsilon\in \mathcal{R}_\Sigma\)

  • \(a \in \mathcal{R}_\Sigma\) for each \(a \in \Sigma\)

  • \(R \in \mathcal{R}_\Sigma \implies (R)^* \in \mathcal{R}_\Sigma\)

  • \(R_1, R_2 \in \mathcal{R}_\Sigma \implies (R_1R_2) \in \mathcal{R}_\Sigma\)

  • \(R_1, R_2 \in \mathcal{R}_\Sigma \implies (R_1 | R_2) \in \mathcal{R}_\Sigma\)

Note that \(\mathcal{R}_\Sigma\) is defined inductively.

Operator Precedence

* comes before concatenation which comes before \(|\).

For example, \(a^*b | bc\) means \(((a^*)b)|(bc)\).

Language of a Regular Expression

The language if a regular expression \(R\), denoted \(L(R)\) is the set of strings that \(R\) matches. Formally,

  • \(L(\emptyset) = \emptyset\)

  • \(L(\epsilon) = \{\epsilon\}\)

  • \(L(a) = \{a\}\), for \(a \in \Sigma\)

  • \(L(R^*) = L(R)^*\) for \(R \in \mathcal{R}_\Sigma^*\)

  • \(L(R_1R_2) = L(R_1)L(R_2)\) for \(R_1, R_2\in \mathcal{R}_\Sigma\)

  • \(L(R_1 | R_2) = L(R_1) \cup L(R_2)\) for \(R_1, R_2\in \mathcal{R}_\Sigma\)

Examples

What are the languages of the following regular expressions? (Assume the alphabet is \(\{0,1\}\))

  • \(((0|1)(0|1)(0|1))^*\)

  • \((1^*01^*0)^*\)

  • \((0|1)^*1(0|1)(0|1)\)

  • \((0|1)^*010(0|1)^*\)

  • \((0 | \epsilon)1^*\)

Solution

  • \(L(((0|1)(0|1)(0|1))^*) = \{w: |w| = 0 \mod 3\}\).

  • \(L((1^*01^*0)^*) = \{w: w \text{ ends with 0 contains an even number of 0s}\}\).

  • \(L((0|1)^*1(0|1)(0|1)) = \{w: \text{ third last character of $w$ is 1}\}\).

  • \(L((0|1)^*010(0|1)^*) = \{w: w \text{ contains 010}\}\).

  • \(L((0 | \epsilon)1^*) = \{w: w \text{ is zero or more 1s or 0 followed by zero or more 1s}\}\).

Shorthand

If \(R\) is a regex, and \(m \in \mathbb{N}\), then

  • \(R^{m}\) means \(m\) copies of \(R\).

  • \(R^{+} = RR^*\), i.e. at least one copy of \(R\).

  • \(R^{m+} = R^mR^*\) means at least \(m\) copies of \(R\).

If \(S = \{s_1,s_2,...,s_n\}\) is a finite set of strings, then \(S\) is shorthand for \(s_1 | s_2 |...| s_n\). A common one is to use the alphabet, \(\Sigma\).

Examples

Write regular expressions for the following languages

  • Starts with 010.

  • The second and the second last letter of w are the same.

  • Contains 110.

  • 1s always occur in pairs.

  • Doesn’t contain more than four 1s in a row.

Solution

  • Starts with 010. \(010\Sigma^*\)

  • The second and the second last letter are the same. \(\Sigma0\Sigma^*0\Sigma | \Sigma1\Sigma^*1\Sigma\)

  • Contains 110. \(\Sigma^*110 \Sigma^*\)

  • 1s always occur in pairs. \(\{0,11\}^*\)

  • Doesn’t contain more than four 1s in a row. \(\{0,01,011,0111, 01111\}^*\)