Lecture 09: Formal Language Theory 1
2025-06-04
Formal languages
Reference
This lecture loosely follows chapter 1 of Introduction to the Theory of Computation by Michael Sipser.
The presentation there is a little more formal, but we’ll use the same notation so it might be useful to check that out for additional examples.
Problems
In lecture 1 we used Cantor’s Theorem to show that there are problems that can’t be solved. In that lecture, we defined a problem for every set.
If \(A\) is a set of strings, there is the problem problem of deciding whether a given input is in \(A\) or not.
Examples: \[ A = \{w \in \mathrm{Strings}: w \text{ is a palindrome}\}, \]
\[ A = \{w: w \text{ is a C program with no syntax errors}\}. \]
Formal Languages
The problems that we consider are still going to be of this type!
This time, we’ll make things a little more formal...
Definitions
An alphabet, \(\Sigma\) is a non-empty, finite, set of symbols.
A string \(w\) over an alphabet \(\Sigma\) is a finite (0 or more) sequence of symbols from \(\Sigma\).
The set of all strings is denoted \(\Sigma^*\). (Before now, we’ve been calling it \(\mathrm{Strings}\)).
A language is any subset of \(\Sigma^*\).
Denote the empty string by \(\epsilon\) and note that it is the unique string with length \(0\).
More definitions
Let \(x, y \in \Sigma^*\) be strings, \(A, B \subseteq\Sigma^*\) be languages, and \(n \in \mathbb{N}\) be a natural number
Write \(xy\) to mean the concatenation of \(x\) and \(y\).
Write \(x^n\) to mean \(\underbrace{xx...x}_{n \text{ times}}\).
What is \(x^0\)?
Solution
\(\epsilon\).Let \(AB = \{ab: a \in A, b\in B\}\).
Let \(A^n = \underbrace{AA...A}_{n \text{ times}}.\)
What is \(A^0\)?
Solution
\(\{\epsilon\}\).- Let \(A^* = A^0 \cup A^1 \cup A^2 \cup A^3 \cup ... = \bigcup_{i \in \mathbb{N}}A^i\)
Generated by...
A while ago we studied what it meant for a set to be generated from \(B\) by the functions in \(F\).
Question. How would you generate \(\Sigma^*\)?
Solution
\(B = \Sigma \cup \{\epsilon\}\)
\(F = \{\texttt{concat}\}\)
Example - English
\(\Sigma = \{a, b, c,...,z\}\)
\(\Sigma^* = \{\epsilon, a, aa, ab, ac,...,ba,...,aaa,...\}\)
\(\mathrm{English} \subseteq\Sigma^*\)
Example - Even
\(\Sigma = \{0,1\}\)
\(\Sigma^* = \{\epsilon, 0,1,00,01,...\}\)
\(\mathrm{Even} = \{w \in \Sigma^*: w \text{ has an even number of 1s}\}\)
Alphabet
Any finite set works for the alphabet! However, to make things simple, we’ll usually take the alphabet to be \(\Sigma = \{0,1\}\), or \(\{a, b\}\).
The Problem (again)
Given a language \(A\) over an alphabet \(\Sigma\), come up with a program that decides whether a given string \(x \in \Sigma^*\) is in \(A\) or not.
Deterministic Finite Automata
What is a program?
To talk formally about computation it’s important to specify a model of computation.
What does a program look like?
What can the program do?
DFAs
DFAs are one model of computation. They look like this.
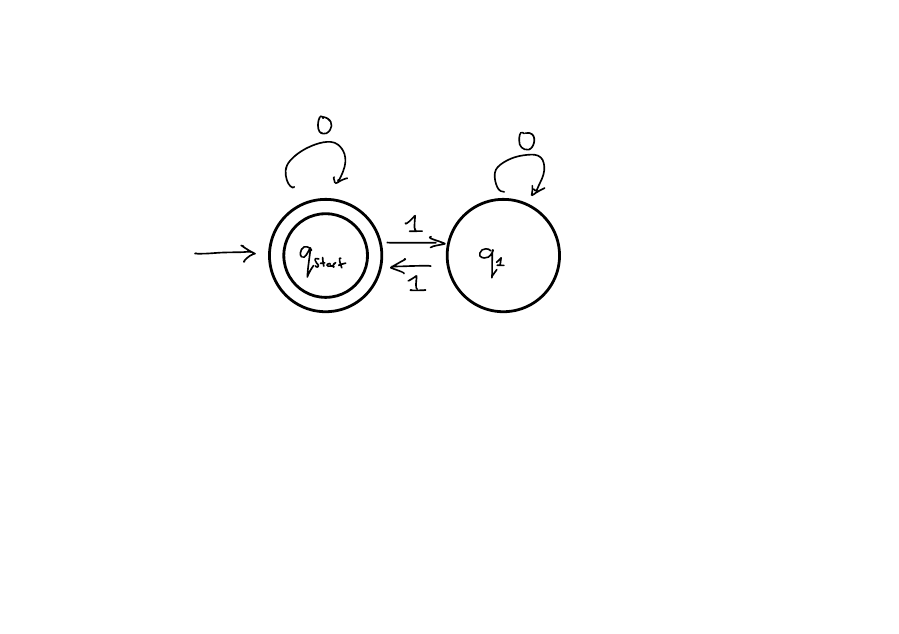
A single DFA corresponds to what we think of as a program.
Computation of a DFA
Input: a string \(w \in \Sigma^*\).
Output: accept/reject.
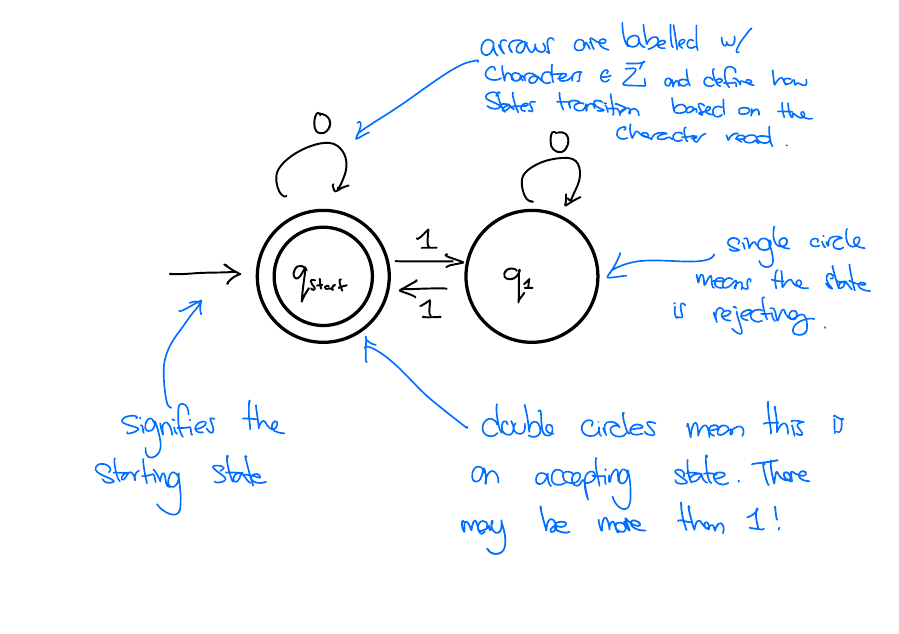
The DFA starts at a predefined start state.
The DFA reads in the input string one character at a time. Depending on the character read and the current state, the DFA deterministically moves to a new state.
When it has read the entire string, the DFA will be in some state. If that state is one of the accept states, the DFA accepts. Otherwise, the DFA rejects.
Language of a DFA
Let \(M\) be a DFA, the language of a DFA, denoted \(L(M)\), is the set of strings \(w \in \Sigma^*\) such that \(M\) accepts \(w\).
Example

Example
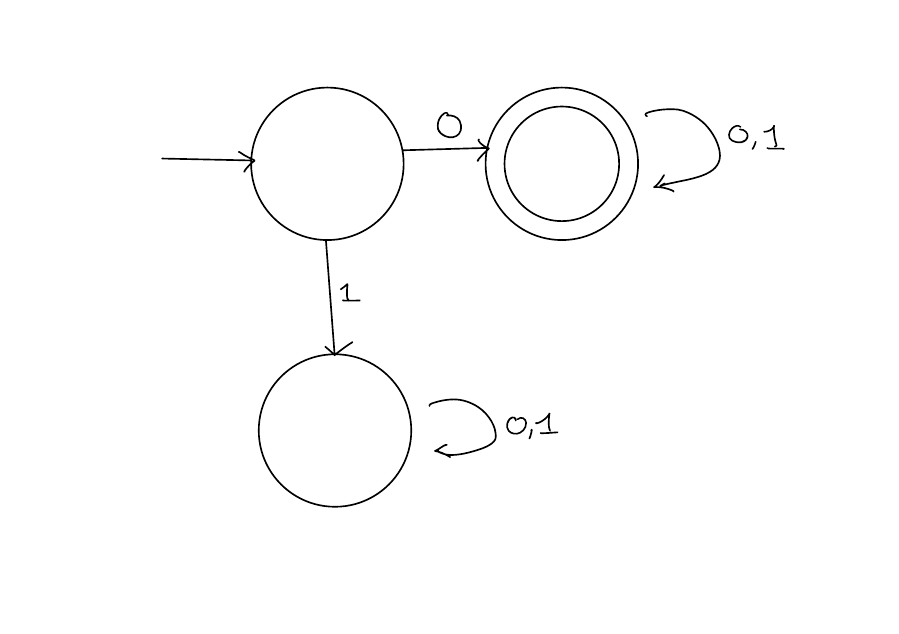
Example
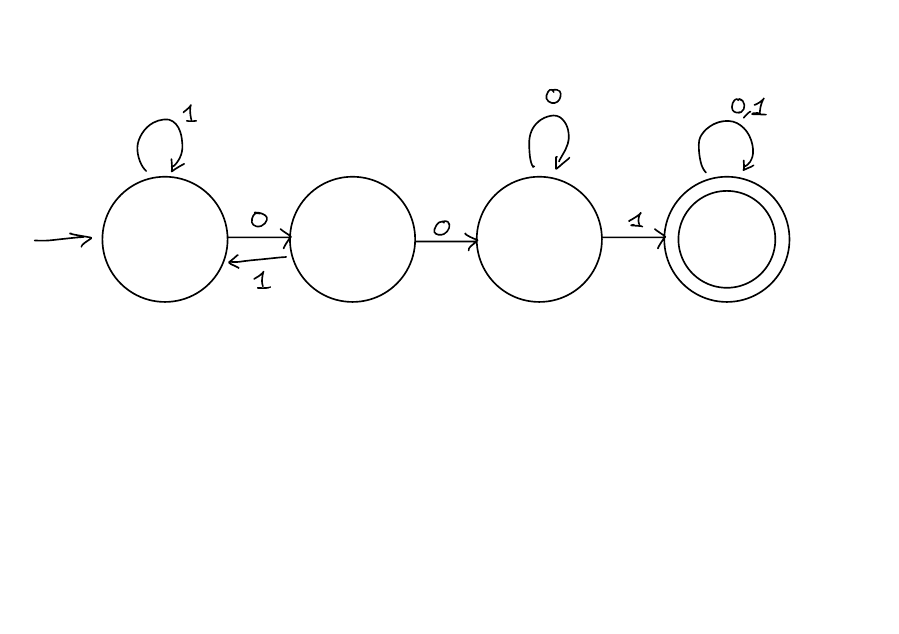
Example
DFAs
Deterministic. Given the current state and character read, the next state is always the same.
Finite. There are a finite number of states.
States are analogous to “memory”, since we can store information about the input by transitioning to different states.
Designing DFAs
Defining a DFA
When defining a DFA, you need to do the following
Tell me the alphabet, \(\Sigma\) of the DFA.
Define a finite set of states, \(Q\).
Tell me a start state \(q_{\text{start}} \in Q\).
Tell me which states are accepting. Formally, find a subset \(F \subseteq Q\) of accept states.
For each state \(q\) and each character \(x \in \Sigma\), tell me which state to go to next if I read \(x\) from state \(q\).
In this class, you may capture all of this information in a drawing.
Tips
States \(\iff\) Memory. Use states to capture information about the input read so far! What do you need to remember about the input in order to answer the question?
It takes some time getting used to the fact that we read the input left to right, and only get to read each character once! Keep this in mind when designing DFAs!
Common pattern: The garbage state.
Example
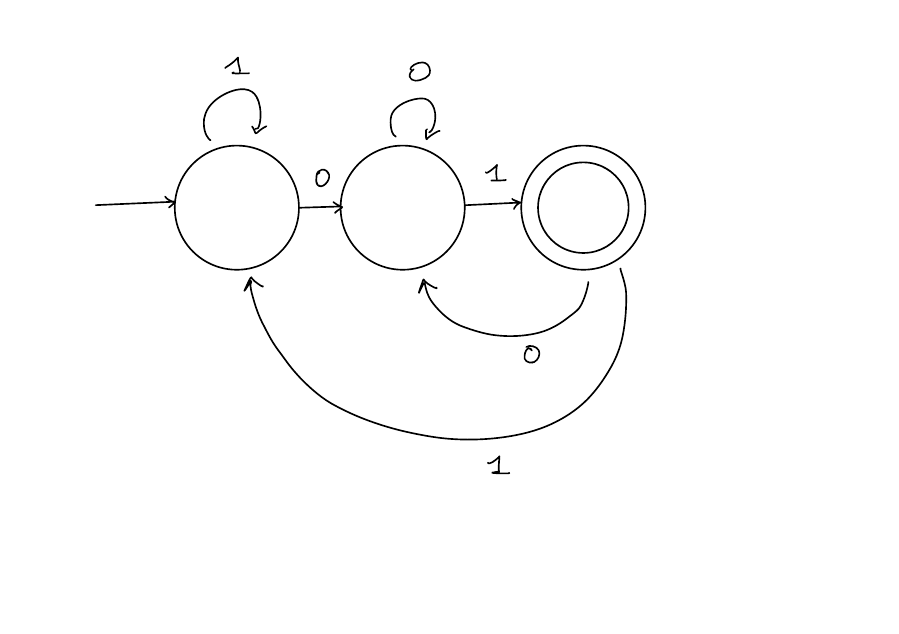
Design a DFA \(M\) such that \[ L(M) = \{w \in \left\{0,1\right\}^*: w \text{ has at least two 1s}\} \]
Solution
Example
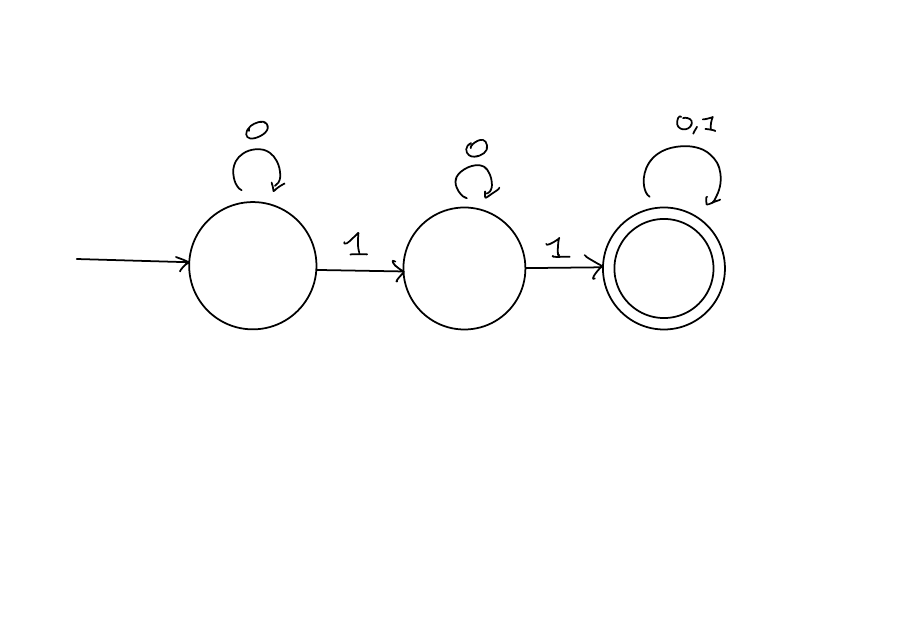
Design a DFA \(M\) such that \[ L(M) = \{w \in \left\{0,1\right\}^*: w \text{ does not contain the substring 11}\} \]
Solution
Example
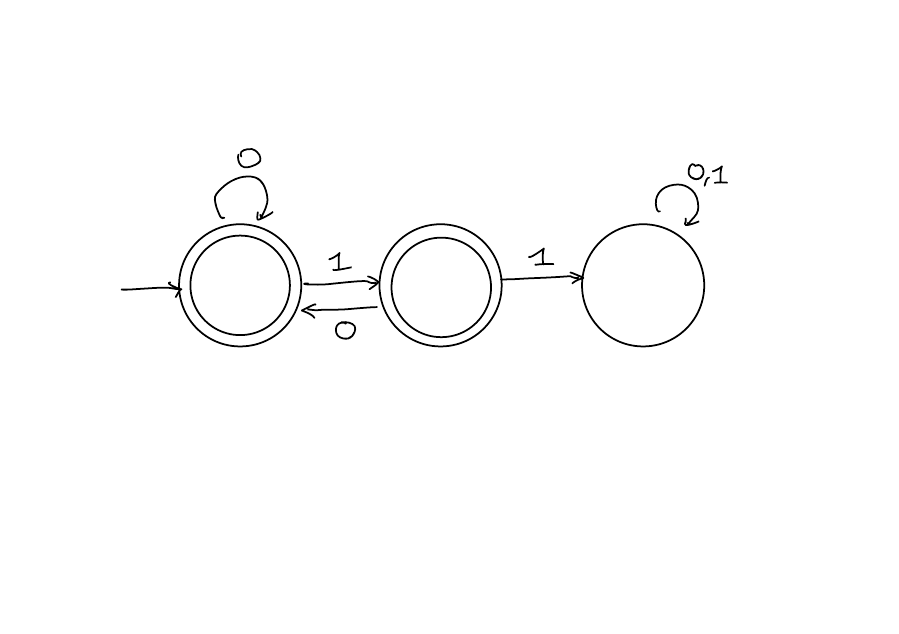
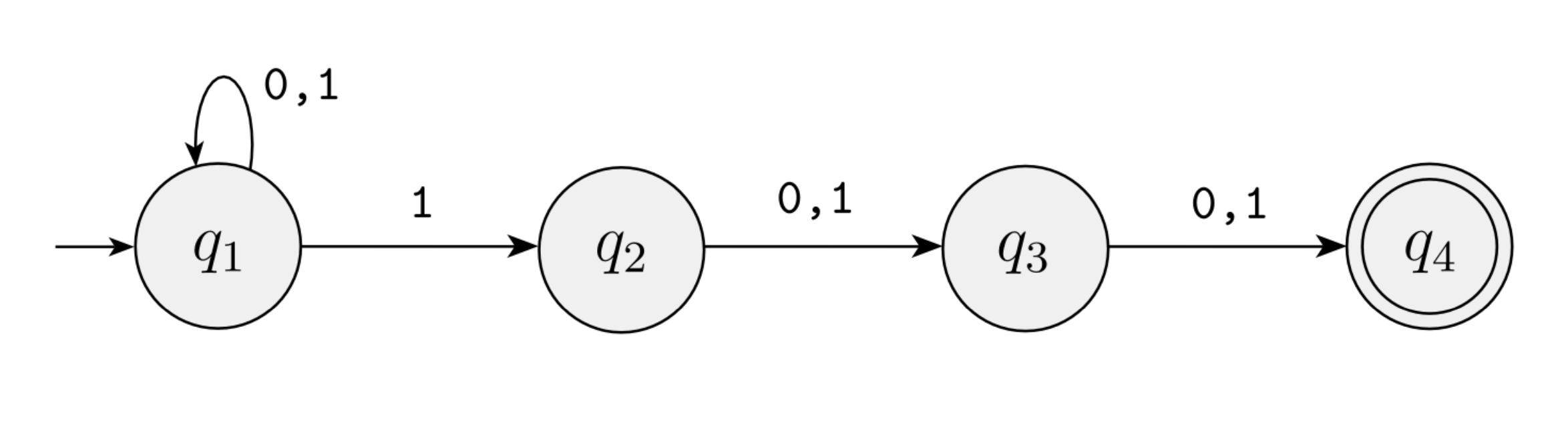
Design a DFA \(M\) such that \[ L(M) = \{w \in \left\{0,1\right\}^*: \text{ The third last character of $w$ is 1}\} \]
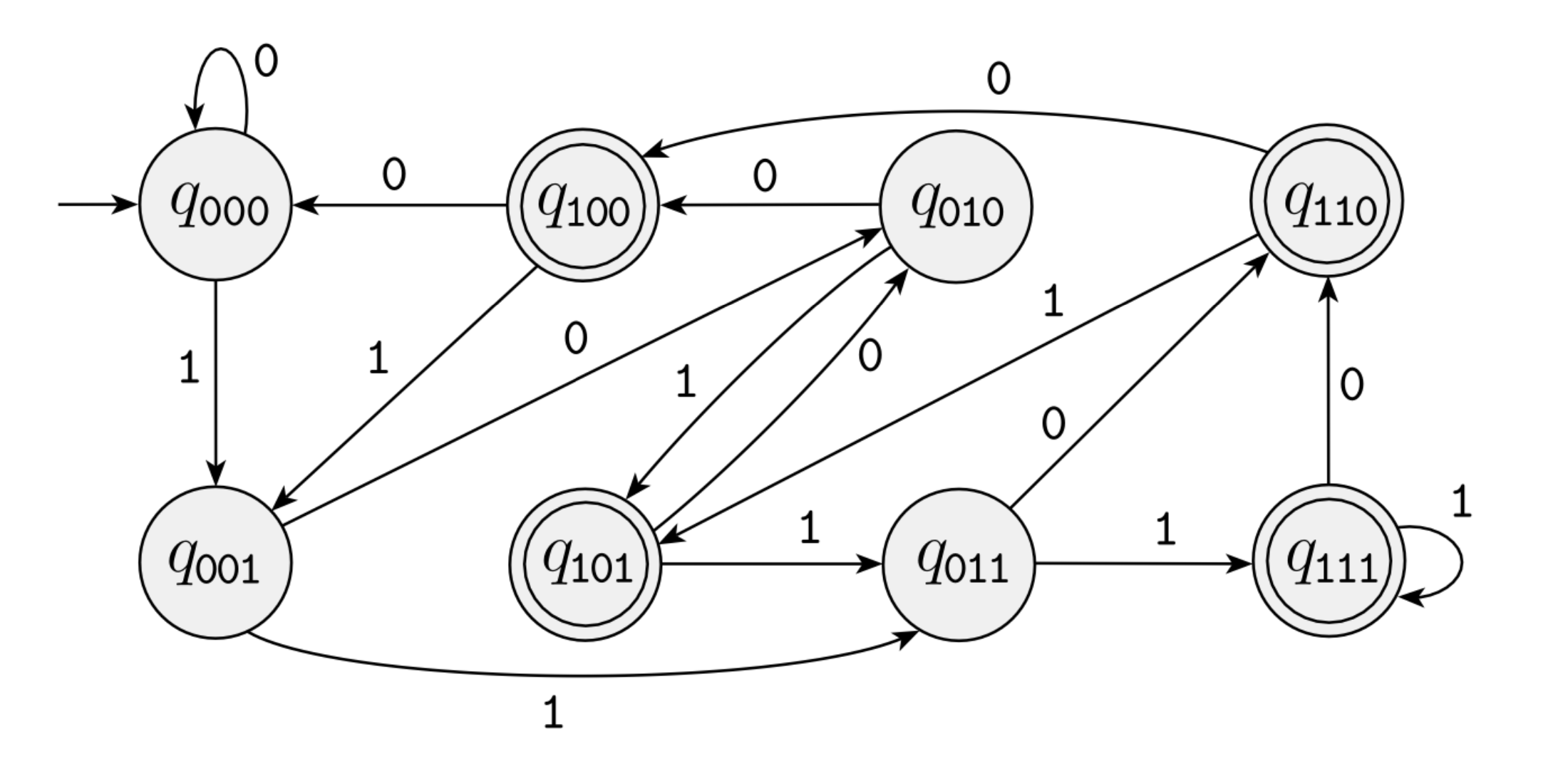
Reference: Sipser
Non-Deterministic Finite Automata (NFAs)
Another model of computation - Nondeterministic Finite Automata (NFAs)
Here’s an example of an NFA 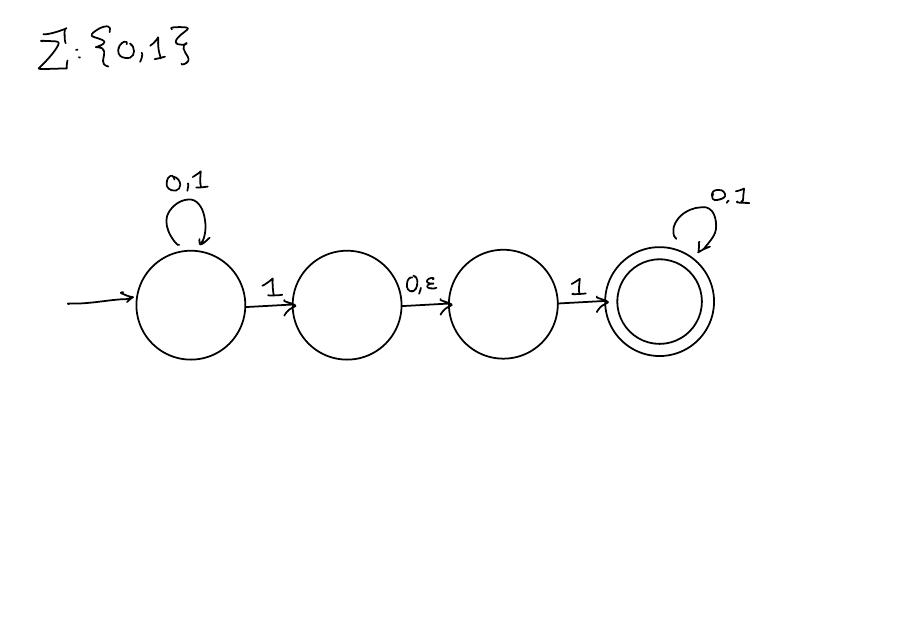
Key differences
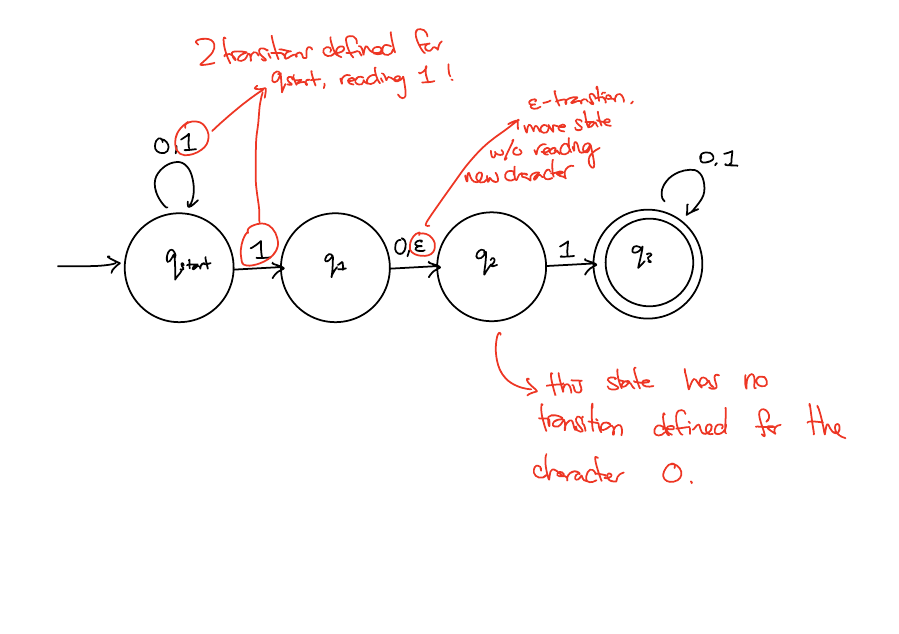
For each state, there can be multiple arrows labelled with the SAME character!
States do not need to have one arrow for each character in \(\Sigma\).
Arrows can be labelled with \(\epsilon\).
Computation of a NFA
Input: a string \(w \in \Sigma^*\).
Output: accept/reject.
The NFA starts at a predefined start state.
The NFA reads in the input string one character at a time. Let \(c\) be the character that was read. There are several cases depending on the current state.
If the state has no arrows coming out of it labelled with \(c\), halt execution and immediately reject.
Otherwise, choose one of the arrows labelled with \(c\) and follow it and read the next character.
If there is an arrow labelled with \(\epsilon\), you may choose to follow it. In this case, you don’t read the input character (i.e. the next character to be read is still the same)
When it has read the entire string, the NFA will be in some state. Depending on the choices made, the final state will either be accepting or rejecting. The NFA accepts the string if ANY sequence of choices leads to an accept state.
Language of a NFA
Let \(N\) be a NFA, the language of a NFA, denoted \(L(N)\), is the set of strings \(w \in \Sigma^*\) such that \(N\) accepts \(w\).
What is the language of...
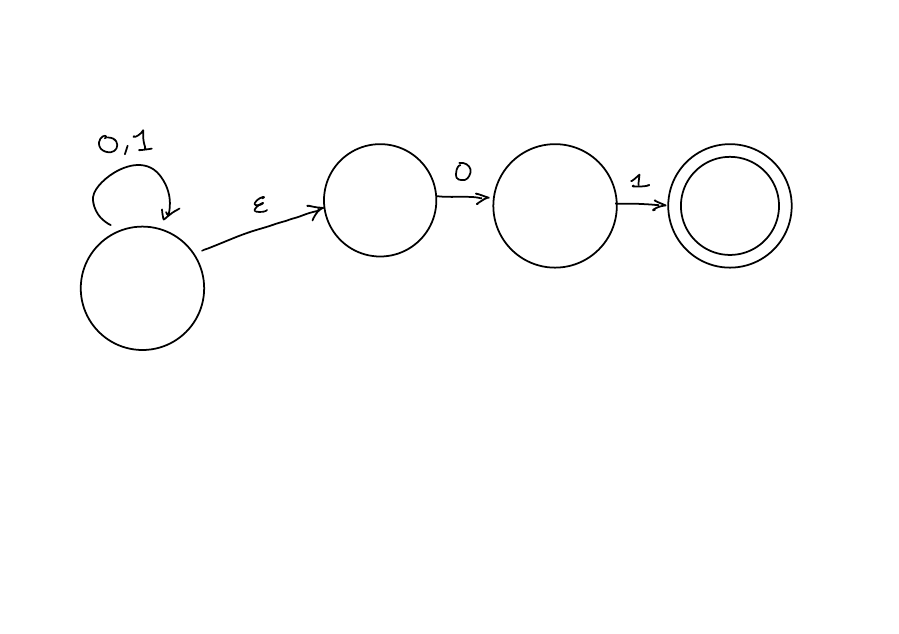
Solution
\(\{x: x \text{ ends with 01}\}\)
Common Pattern
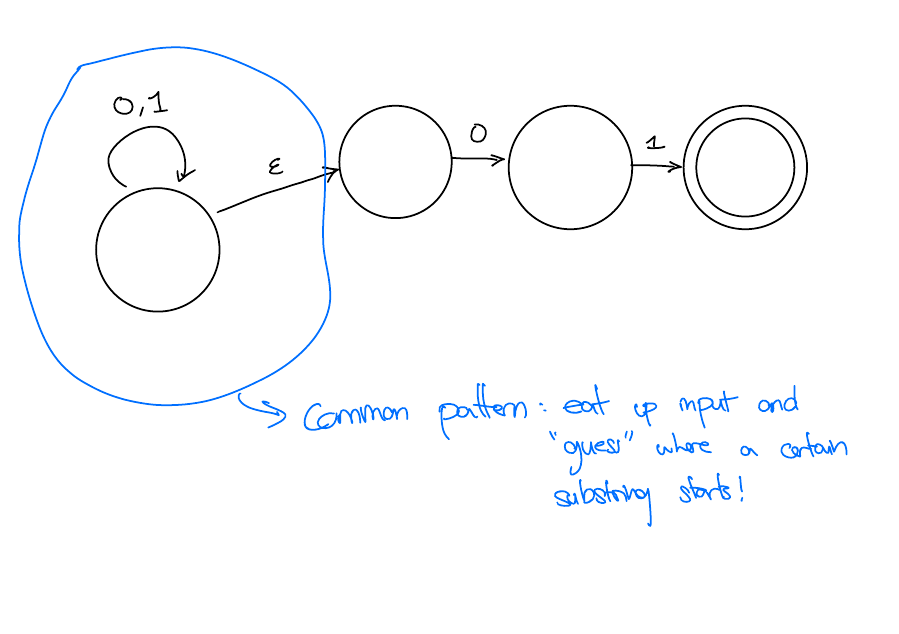
NFA for third last character is a 1
CSC236 Summer 2025