. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
be the first-order ODE.
Note that 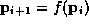 is the solution of (9)
using
is the solution of (9)
using 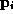 as the initial condition and integrating
as the initial condition and integrating 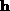 to time
i+1. Then
to time
i+1. Then 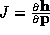 is the Jacobian of
is the Jacobian of
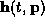 . The Jacobian measures how
. The Jacobian measures how 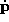 changes if
changes if
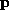 is changed by a small amount. The resolvent
is changed by a small amount. The resolvent 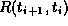 is the integral
of J(t) along the path
is the integral
of J(t) along the path 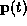 , and describes how a small perturbation
, and describes how a small perturbation
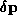 from
from 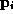 at time
at time 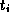 gets mapped to a perturbation
from
gets mapped to a perturbation
from 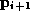 at time
at time 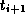 . That is,
. That is, 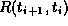 is the solution of the variational equation
is the solution of the variational equation
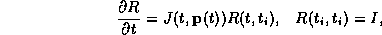
where I is the identity matrix.
The reason the arguments to R seem reversed is for notational
convenience: they satisfy
the identity 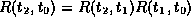 , and so a perturbation
, and so a perturbation
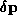 at time
at time 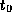 gets mapped to a perturbation
at time
gets mapped to a perturbation
at time 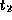 by the
matrix-matrix and matrix-vector multiplication
by the
matrix-matrix and matrix-vector multiplication
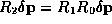 [30].
Finally, the linear map in the GHYS refinement procedure is
[30].
Finally, the linear map in the GHYS refinement procedure is
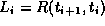 .
.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
 -shadows a noisy orbit, there exist infinitely many
true orbits nearby that also shadow it.
However, it may be that all the true orbits are packed into a space
unresolved by the machine precision.
-shadows a noisy orbit, there exist infinitely many
true orbits nearby that also shadow it.
However, it may be that all the true orbits are packed into a space
unresolved by the machine precision.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

where 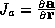 is symmetrical, and has real but not necessarily
positive eigenvalues. If
is symmetrical, and has real but not necessarily
positive eigenvalues. If 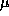 is an eigenvalue of
is an eigenvalue of 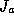 , then
, then
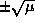 are eigenvalues of J. If
are eigenvalues of J. If 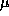 is positive, this
gives one expanding and one contracting direction; if
is positive, this
gives one expanding and one contracting direction; if 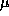 is negative,
it gives directions that neither expand nor contract, but ``rotate'' in
some sense. These are the directions that are non-hyperbolic.
is negative,
it gives directions that neither expand nor contract, but ``rotate'' in
some sense. These are the directions that are non-hyperbolic.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
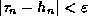 .
.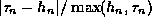 in case
in case 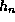 or
or 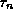 gets too small.
gets too small.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
