Teaching
For a complete list of my teaching experience, see the home page. Here are some teaching materials I have developed over the years.CSC236 (Introduction to the Theory of Computation)
I am the current (Summer 2025) course instructor for CSC236. You can find the course webpage here.
Here is the course webpage for when I taught the course in Summer 2023.
Notebooks + Coding Projects
For CSC373 (Algorithms, Design and Analysis)
These notebooks accompany the undergraduate algorithms course at U of T. I developed them when I taught the course in 2024.-
Huffman
Coding and Closest Pair in
-
In this notebook, students implement two algorithms from class: Huffman Coding and the Closest
pair
in
- There are visualizations for both algorithms
-
For the closest pair in
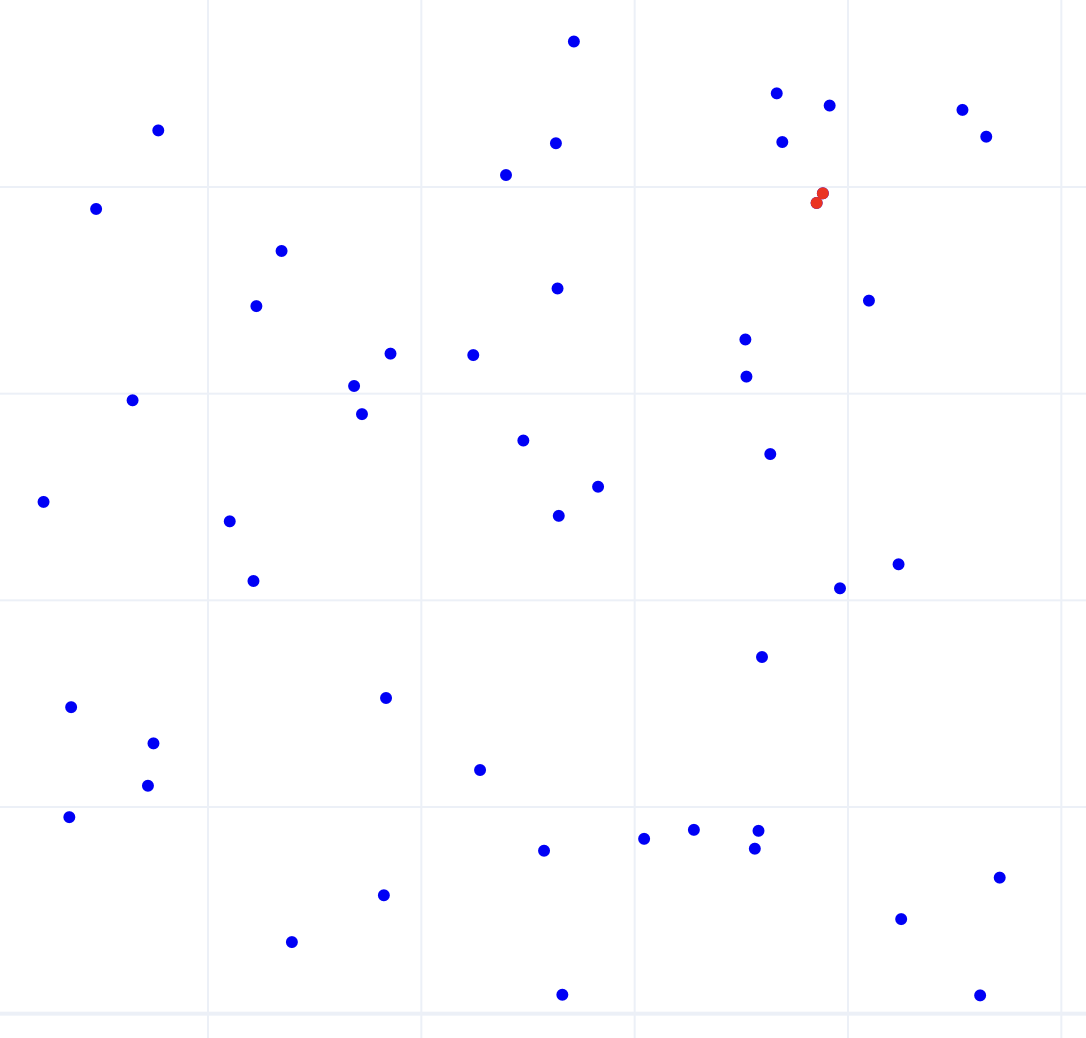
-
In this notebook, students implement two algorithms from class: Huffman Coding and the Closest
pair
in
-
Dynamic
Programming
- In this notebook, students implement DP algorithms for the knapsack problem and the traveling salesman problem.
- Students who completed the Journey through Hoenn notebook in 236 will now be able to find an exact solution (instead of an approximate one)!
-
Flow and LP
- In this notebook, students model and solve matchmaking problem - matching CS students with business students for a group project.
- The unweighted version (maximum cardinality matching) is solved via max flow
- The weighted version is solved via LP
- Python libraries networkx and scipy are used to solve max flow and linear programming respectively.

For CSC236 (Introduction to the Theory of Computation)
-
A
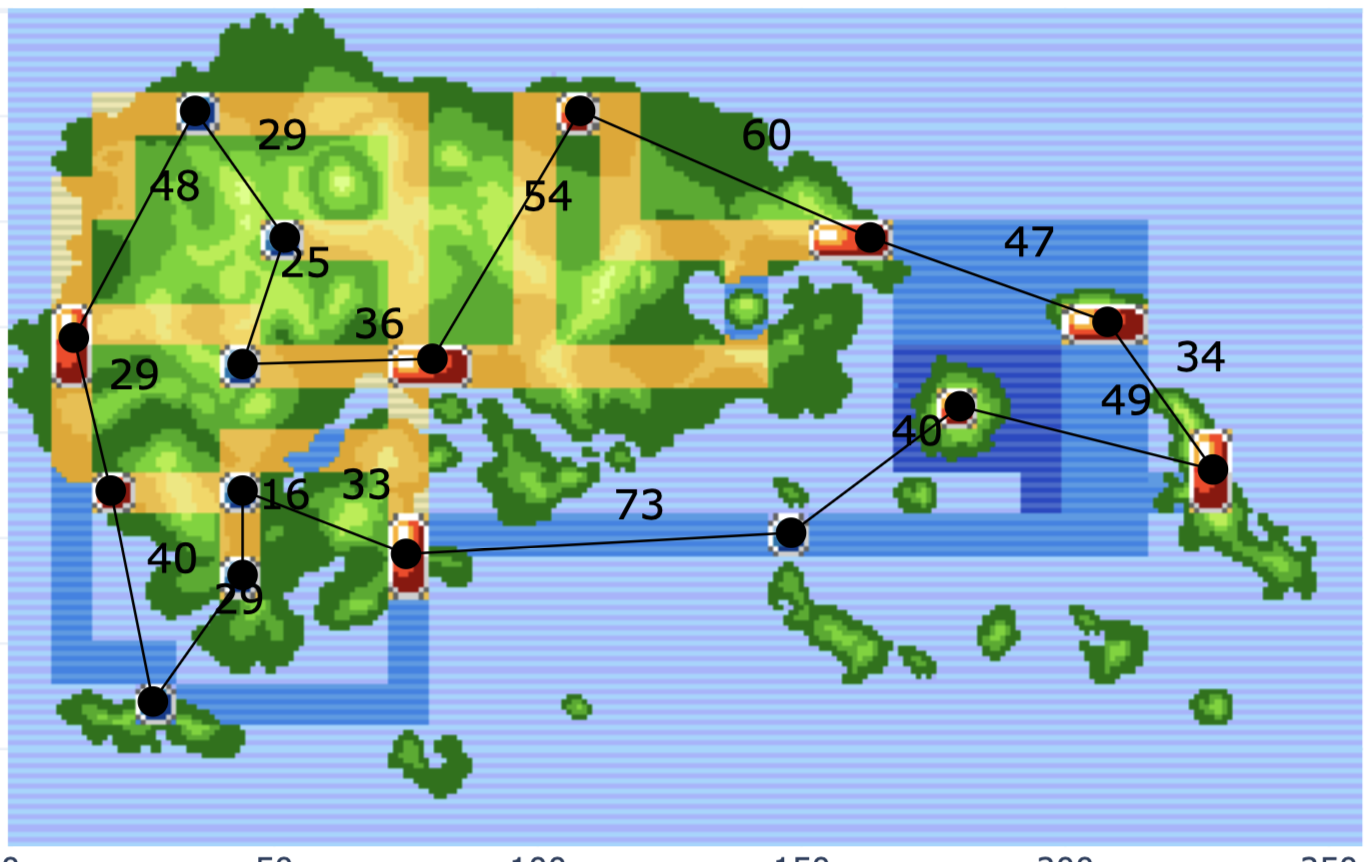
Journey Through Hoenn
- In this notebook, students model the problem of finding the quickest way to visit each city in the City of Hoenn (from Pokemon Emerald) as a graph problem and approximate a solution using the networkx library
- There are variants for where you can move in any direction and where you can move only up/down/left/right.
- As a bonus, the notebook explores a relaxation of the problem where backtracking is `free.` I.e. If I have visited a city before, I can fly to it again at zero cost. This variant can then be modeled by another well-known graph problem.
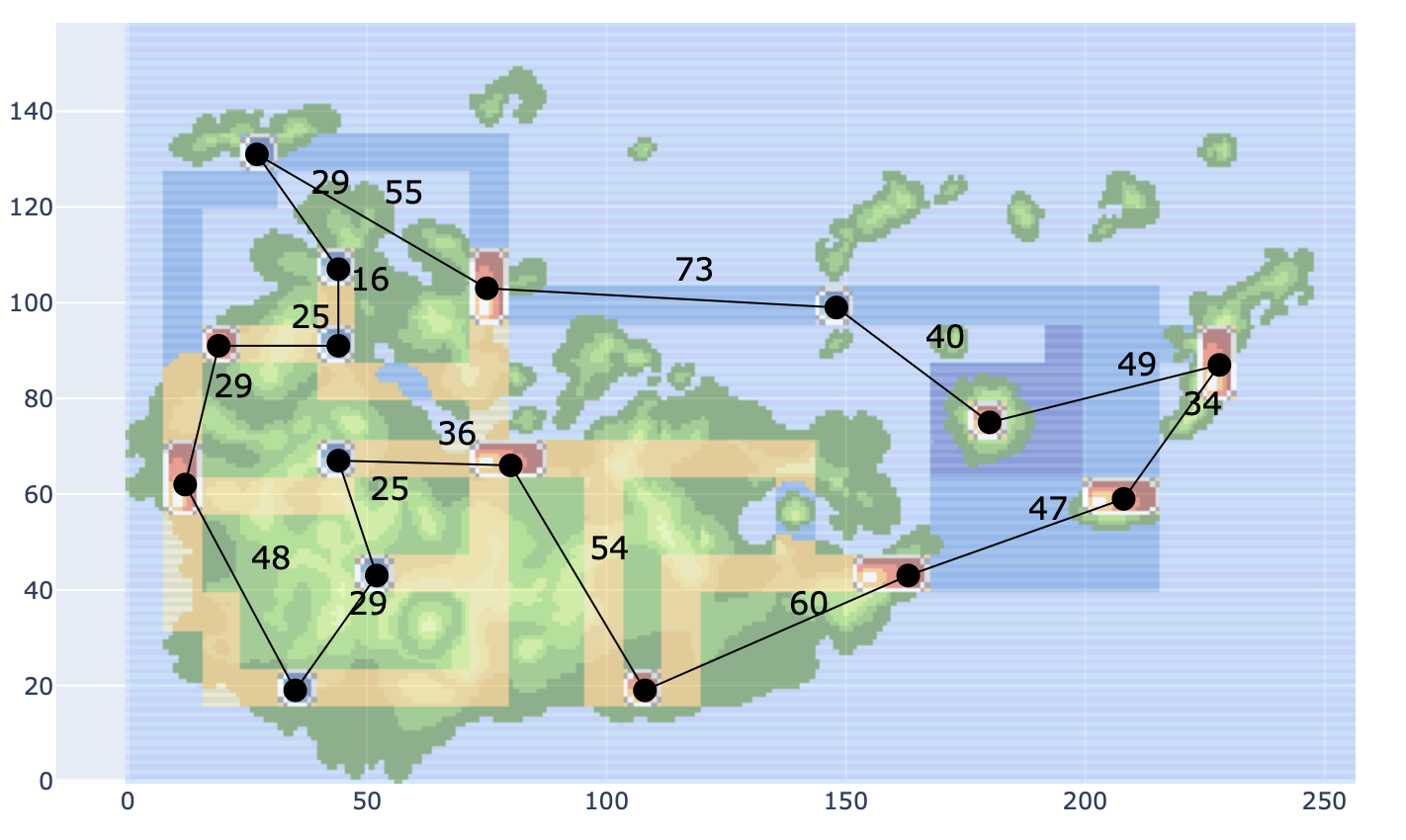
For Inspirit AI
These are notebooks I developed for Inspirit AI. These projects are for students at the high school and middle school levels.-
Self driving cars: 1, 2, 3
- In this project, students gradually build models to drive cars in one of the OpenAI Gyms environments.
- The project starts with basic models to decide whether the road turns left or right and gradually builds to models based on behavioral cloning and deep Q-learning.

- Covid mask detection: 1,
2, 3
- In this project, students build models to detect whether or not someone is wearing a mask.
- The models start very simple (using the color distribution of the input image) and gradually get more complex, building up to a convolutional neural network with a facial recognition preprocessing step.
- Students then get a chance to test the model on their images.
-
Game playing AI -
the minimax algorithm and variants
- Students implement the minimax algorithm and use it to play tic-tac-toe and connect 4.
- Students tune a heuristic evaluation function and then get to play against their algorithm, which is always fun :)
