Chow and Palmer [14] provide a proof of the shadowing
lemma in 1 dimension when f is a (non-uniformly) expanding map.
(Recall that if f is expansive in forward time, then it is contractive
in reverse time. Thus we want f to be as expansive as possible when
iterated forward, i.e., we want 
to be as small as possible, to
facilitate shadowing.)
Let 
be a pseudo-orbit of a 
continuous
map 
.
They define the ``expansiveness'' as
Each 
measures how contractive the map is when applied
backwards at step i, so that smaller is ``better''.
So, each term in the sum measures how contractive the map
is when applied backwards from step m down to n.
Thus, the larger the sum of absolute values is, the less
contractive the map is, when applied backwards from any
point beyond n, down to n. Finally, the supremum measures how
non-contractive the map can be anywhere. The larger 
is,
the less contractive the inverse map 
is, and
the more difficult it is to shadow the orbit.
Then they define a term I would call the ``error diminishing factor'':
where 
is the 1-step error of step m+1. The
description is similar to that of . For example, the n=0 term
measures by how much all the 1-step errors are contracted when they are
propagated backwards to step 0.
THEOREM[14]: Let be a
function with
Let 
be a pseudo-orbit of f such that
Then there is an exact orbit 
with
OUTLINE OF PROOF: We will not discuss the lower bound except to note the interesting fact that it says that the shadow can not be arbitrarily close to the noisy orbit. It is the upper bound that concerns us.
Let the 1-step error at each step be
and let 
be the offset from the noisy
orbit to the true orbit we will find, 
.
The 
are
analogous to the correction terms 
of the GHYS/QT refinement algorithm
defined in equation (7).
Then we find that the need to satisfy
where
measures the quality of the 1st order Taylor approximation to 
,
so 
for small z.
It comprises the terms we ignored in equation
(7) that go to zero as 
approaches a true orbit.
Denote by S the set of sequences with 
for all n. The following mapping T is analogous to 1 refinement
of the GHYS/QT algorithm, with the boundary condition 
.
However, it includes, via 
,
the second-and-higher order terms ignored by GHYS/QT, so that if one
could actually construct T, it would find the exact shadow in a
single ``refinement'' iteration:
Chow and Palmer go on to show that T maps S into itself by showing
that 
and hence that 
is
bounded by 
. Finally, since
T maps S into itself, they invoke Brouwer's Fixed Point Theorem
to prove that there is a fixed
point 
of T, proving that a shadow exists within 
Since computing and 
in full would be very expensive
( 
time), they instead compute
where p is a positive integer chosen as follows. For 
,
we define
Then we choose the smallest p so that 
. What 
says
in words is, ``ensure that any sequence of p iterations of ,
taken as a unit, perform a contraction''. Said another way, if ,
then there does not exist an expansive sequence of backwards iterations
of f lasting longer than p. Thus, all backwards sequences of iterations of
f longer than p will be contracting, so that, as a whole, the
trajectory is ``shadowable''. The larger p is, however, the less
shadowable the trajectory becomes until, if 
, there is too
little hyperbolicity. Using a similar argument they define a 
,
using the same p as above.
Finally, Chow and Palmer apply this algorithm to the quadratic map
They show that with a=3.8 and 
, they can choose p=30, and
can shadow the orbit for N=426,000 iterates, with a shadowing distance
of 
.
They also perform a detailed analysis of roundoff errors to ensure
that their bound is completely rigorous, but we do not detail
their analysis here.
Hadeler [29] relates Chow & Palmer's
one dimensional Shadowing Lemma to the older and more well
understood work related to Newton's method and Kantorovich's theorem.
Kantorovich's theorem is a statement relating G, G', 
and
an initial guess 
to the convergence of Newton's method.
Hadeler shows how to translate between Chow & Palmer's Shadowing
Lemma and Kantorovich's theorem, showing the relation between
the former's and quantities to quantities needed
in order for Kantorovich's theorem to hold. This means that we
are closer to being able to apply the vast amount of literature
related to Newton's method to shadowing.
Chow and Palmer extended their analysis to maps in higher dimensions
[15]. Although the details are different for the
multidimensional case, the basic idea is the same as the one dimensional
case. Letting be a true orbit offset by from the
noisy orbit , one defines an operator L that computes 1-step errors
from offsets:
where Z is the set of possible offsets and E is the set of possible
1-step errors. Note that if the space is D dimensional and there
are N points in the orbit, then 
, but
, so L is many-to-one.
(This is not surprising: there are many different noisy orbits that
can possess the same set of 1-step errors.)
Finally, our task is to solve 
. However, since L is
many-to-one, 
is not unique and our task is to choose the
with smallest norm, so that 
is minimized.
Chow and Palmer show that if the map has strong hyperbolicity, then
the with smallest norm is the one that we would expect if
we understand the GHYS/QT algorithm: after decomposing space into
the stable and unstable subspaces, 
has zero component in
the stable subspace, while 
has zero component in
the unstable subspace. They demonstrate their
method on the Hénon map, and show that for a noisy orbit in double
precision with 1-step errors of 
,
they can use p=40 and shadow N=333,000 iterates with an
. This means that the shadowing
distance is about 
times the size of the
1-step errors, giving a shadow distance of about 
.
This ``magnification factor'', the ratio between shadow distance and
local error, is termed the ``brittleness'' of an orbit by Dawson et al.
[20]. They show that if the number of
positive and negative Lyapunov exponents changes, or if a particular
one fluctuates about zero, then this magnification factor can blow
up. If the brittleness is of order the inverse of the machine
epsilon, then all accuracy is lost as the shadowing error is
comparable to the size of the variables themselves. The reason
that a fluctuating exponent is bad is related in the following diagram,
where 
is the local error, and the vertical direction is
initially contracting, but then becomes expanding (Figure 3).
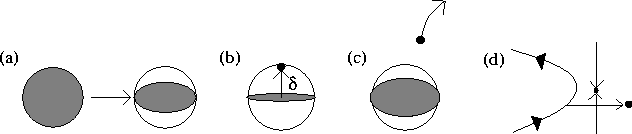
Figure: FLUCTUATING LYAPUNOV EXPONENT IN THE "VERTICAL" DIRECTION.
As we see, (a) an ensemble of trajectories that starts off in an 
-ball
is first compressed into a sheet. (b) If the local error steps outside
this sheet, and then the direction becomes an expanding direction, then
(c) the numerical trajectory diverges away from all true trajectories that
started in the original -ball, (d) possibly entering regions of
phase space with qualitatively different behaviour than the true
trajectories.
However, Dawson et al. make the strong claim that they believe this kind of fluctuation of Lyapunov exponents is ``common'' in high dimensional systems, with the only justification apparently being that there are so many dimensions, there must be a fluctuating exponent somewhere. It is unclear if this argument applies to all systems. For example, Hamiltonian systems always have equal numbers of positive and negative exponents.