Glossary

Like most groups of technical people, stellar dynamicists have a language all their own. This glossary is informal, and constitutes an exceedingly brief and fleeting crash course in stellar dynamics for those members of my committee not familiar with the terms. It is designed to be read sequentially, not alphabetically.

collision

A collision occurs when two particles pass close enough to each other to ``substantially'' alter at least one of their pre-encounter paths. They don't actually have to ``touch'' in any physical sense. If they are part of a larger parent body (eg.,  a galaxy) then their orbits will also be altered. The definition of ``substantial'' depends on context, but most real gravitational systems are either clearly collisional (eg.,  globular clusters) or collisionless (most galaxies). No system is completely collisionless, but galactic disks, for example, have relaxation times that are orders of magnitude longer than the age of the universe.

encounter

An encounter is a term that applies to any 2-body interaction. Although collision and encounter are often used interchangeably, a collision usually refers explicitly to a close or strong encounter.

crossing time

The average time it takes a body to travel from one side of the system to the other, sometimes defined as

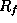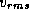where is the radius of a sphere that contains a fraction f (usually 1/2) of the mass of the system, and is the root mean square particle speed. In disk systems, it is half the average orbital period.

relaxation

In a real system, each particle has a birth date (eg.,  the formation of a star from a condensing gas cloud), at which time it enters an initial orbit. As the system ages, particles are perturbed from their initial orbits both by the slowly changing global potential, and by collisions. The process acting on individual particles is similar to a random walk; the cumulative effect on the system is called relaxation. A system is relaxed when no information remains about the initial orbits of most particles. More formally, if we look at the collisions experienced by a single particle and 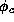is the deflection in radians caused by each collision c, then if most particles satisfy

 

then the system is relaxed. Similar arguments can be made for the relative change in orbital energy or orbital angular momentum per collision. A slightly more detailed analysis [9, chapter 4,] shows that the relaxation time is about 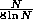crossing times.

equipartition

Each particle has kinetic energy (v measured relative to the centre of mass of the entire cluster of objects). When two stars of unequal mass collide, they tend to exchange energy so as to equalize their kinetic energies. (This is the same principle used by interplanetary probes for gravity assists: they gain speed, relative to the sun, by passing close to planets.) This results in lighter particles gaining energy and entering higher orbits while larger ones lose energy and sink towards the centre of the system. If we consider particles to be members of a gas, then their kinetic energy can also be interpreted as their temperature (nothing to do with the surface temperature of an actual star). When the temperature of each particle has become statistically independent of its mass, then the system has achieved equipartition of energy.

cold disk

A cold system is characterized by low RMS collision velocities (i.e.,  low velocity dispersion), and higher temperatures mean higher velocity dispersion. A spherical system cannot be cold because every point in the system has orbits with vastly different velocity vectors passing through it. Only disks can be cold, where nearby orbits have similar orbital vectors and thus low relative speeds. The disks of spiral galaxies are generally cold and collisionless, but they slowly heat up as the system relaxes (over time periods much longer than the current age of the universe).

globular cluster

A small, dense, roughly spherically symmetric group of 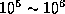old stars. There are about 150 known globular clusters orbiting our Milky Way Galaxy. Since a globular cluster is small and dense, it is highly collisional. The relaxation time of a globular cluster is roughly 3-5 billion years, and they are believed to be composed of the very first stars to form during the formation of our Galaxy about 10 billion years ago; thus existing globular clusters are relaxed (and they are observed to be quite equipartitioned).

spiral galaxy

A group of roughly 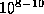stars, arranged with an ellipsoidal centre of old stars and a sparser thin disk of younger stars. The core can be collisional, the disk is generally not.

elliptical galaxy

A voluminous group of roughly 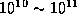stars. They look a lot like globular clusters but are many orders of magnitude larger, sometimes having diameters larger than spiral galaxies. They can be collisional in the core, but generally not outside of it.

Plummer model

A popular model used to describe the gravitational potential (and thereby the density of particles) in spherical stellar systems. The Plummer Potential is defined by

where b is the single parameter and 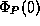gives the potential of a point mass. The gravitational force between two non-overlapping ``Plummer spheres'' is

force softening and discreteness noise

Finally, we are usually restricted to simulate with an N which is many orders of magnitude smaller than the actual number of particles in the system. (For example, even a small globular cluster has 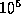members, and it's just possible that we may be able to fully simulate such a system without softening in the next few years.) Thus, each particle in our simulation can be representative of thousands or millions of particles in the real system. Each simulated particle can be interpreted as either A) the total mass of the group it represents, at the centre of mass of the group, or B) a randomly chosen member of that group (``Monte carlo sampling''). In either case the potential energy function of the system is much more ``lumpy'' than it should be, and two-body interactions will be much more important than in the real system. For example, using interpretation (A), two simulated particles passing by each other with zero distance encounter infinite force; whereas in the real system, two groups of particles thrown at each other generally pass through each other almost unscathed. (Because the diameter of a star is about 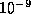of the average distance between them.) This results in the simulated system being much more collisional than the real system, and having a much higher relaxation rate.

A simple method to attempt to partially alleviate this problem is to ``soften'' the force between two simulated particles. The simplest method is to use model (A) and treat the particles as Plummer spheres, replacing Newton's gravitational force law

 

with

 

where is a constant chosen to approximate the average separation between simulated particles. Other methods (like the particle mesh methods, eg.,  [61]) contain implicit softening. However, softening only partially alleviates this problem of discreteness noise. The only known way to substantially improve it is simply to increase N [39].

regularization

If a system is being simulated without softening, then close encounters between particles can occur, and sometimes 3- or more-body interactions can result in the formation of a closed binary or multiple star system. To accurately integrate these tight orbits takes time-steps many orders of magnitude smaller than is typical for non-interacting stars. Multiple star systems form an integral part of the evolution of globular clusters, and thus cannot be ignored. Without special treatment the integration of tight binary star systems can soak up the majority of your CPU time and slow the simulation immensely [1]. Regularization is the process of speeding up the simulation of these orbits by solving them analytically as perturbed two-body systems.

Here are some more terms that are not to do with stellar dynamics, but astronomy in general.

Dark Matter

matter that we can't see, but we know must exist for various reasons, like spiral galaxies rotating so fast that, if the light matter was all that was there, the galaxy would fly apart. Something must be holding it together, assuming gravity is still 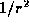at galaxy-sized distances.

Particle-Particle method

the obvious 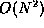method for computing all the forces between all the particles of an N-body system.

Particle-Mesh Method

compute a finite-term expansion of the gravitational potential over a grid (mesh) in space, then interpolate the potential at each particle. The gradient of the potential is the force on that particle.

Tree method

Split the universe hierarchically up into boxes, such that any box containing more than one particle is split into 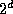equal-sized boxes, where d is the dimension, 2 or 3. Then, when computing the force on a particle, far away particles can be lumped into boxes and an approximate force from all of them can be computed by assuming all the particles are at their mutual centre of mass in the box. The time is 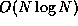to compute all the forces.

Mass segregation

a result of equipartition: massive bodies sink to the bottom of a cluster over time.

Core collapse

a phenomenon, independent of mass segregation (because it happens even if all the masses are the same), whereby energy is transfered out of the core of a collisional system, like a globular cluster. The core gets more and more dense, until, in the limit, it becomes infinitely dense. In reality, core collapse is halted by a mechanism I'm not familiar with, but involves the formation of binary stars in the core.

Perihelion

point of closest approach of a solar system object to the Sun. Also peri-astron, closest approach to any star.

Access count (updated once a day) since 1 Jan 1997: 9518