- ...solutions.
- There is a subspace of measure zero, called the stable subspace,
in which small perturbations do not result in vastly different
solutions. But since it has measure zero, the probability of random
numerical errors being restricted to this subspace is zero.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...time
- The e-folding time
is
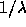 , where
, where 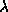 is the Lyapunov exponent.
is the Lyapunov exponent.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...particles.
- This is in stark contrast to N-body simulations
of our solar system, in which case we are interested in the precise
evolution of the particular solar system we live in, not a
hypothetical one very similar to it.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...i+1.
-
In other words, let
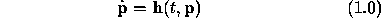
be the first-order ODE. (Often written as y' = f(t,y) in ODE texts.)
Note that 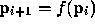 is the solution of equation 1.0 using
is the solution of equation 1.0 using 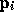 as the initial condition and integrating h to time
i+1. Then
as the initial condition and integrating h to time
i+1. Then 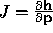 is the Jacobian of equation
1.0. The Jacobian measures how
is the Jacobian of equation
1.0. The Jacobian measures how 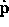 changes if
changes if
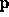 is changed by a small amount. The resolvent
is changed by a small amount. The resolvent 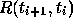 is the integral
of J(t) along the path
is the integral
of J(t) along the path 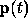 , and tells us how a small perturbation
, and tells us how a small perturbation
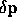 from
from 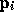 at time
at time 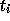 gets mapped to a perturbation from
gets mapped to a perturbation from
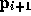 at timestep
at timestep 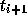 . That is,
. That is, 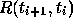 is the solution of the so-called variational equation
is the solution of the so-called variational equation
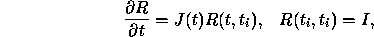
where I is the identity matrix.
(The reason the arguments to R seem reversed is for notational
convenience: they satisfy
the identity 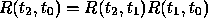 , and so a perturbation
, and so a perturbation
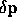 at time
at time  gets mapped to a perturbation
at time
gets mapped to a perturbation
at time 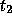 by the
matrix-matrix and matrix-vector multiplication
by the
matrix-matrix and matrix-vector multiplication
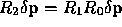 .) Finally, the linear map
in the GHYS refinement procedure is
.) Finally, the linear map
in the GHYS refinement procedure is 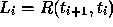 [13].
[13].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...exist.
-
``Proof'': For any system, even a chaotic one, given any true orbit
of fixed length in time, a small enough perturbation in the initial
conditions in any direction produces a small change in the final conditions,
although this perturbation must be exponentially smaller for chaotic
systems than for non-chaotic systems. (If the perturbation is restricted
to the stable subspace, then obviously a similar solution will be obtained.)
Thus given any true orbit that
 -shadows a noisy orbit, we can find infinitely many
other true orbits nearby that also
-shadows a noisy orbit, we can find infinitely many
other true orbits nearby that also  -shadow the noisy orbit.
However, it may be that all the true orbits are packed into a space
unresolved by the machine precision.
-shadow the noisy orbit.
However, it may be that all the true orbits are packed into a space
unresolved by the machine precision.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...SLES
-
SLES is pronounced ``sleeze'', because this seems like such a
sleezy, naïve method.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...orbit,
-
This formulation is not complete,
because we do not yet know how to include the boundary conditions in g.
See further work for more details.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...backwards.
- This oversight is not obvious from the description in their appendix B,
it appears only in their code.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...other.
- If the force is ``softened'', then this problem goes away.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...meaningfully.
- It is trivial to show that the geometric mean of a
set of numbers is the arithmetic mean of their logarithms, to a suitable base.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...RUS.
- For example, with M=25 moving particles, a RUS of length
S=128 requires about 100 megabytes of memory,
and this space scales as
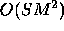 .
((25 particles
.
((25 particles 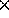 6 dimensions per particle)
6 dimensions per particle)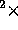 8 bytes
per double precision number
8 bytes
per double precision number 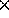 4 (2 resolvents, 2 sets of
basis vectors each covering half the space)
4 (2 resolvents, 2 sets of
basis vectors each covering half the space) 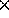 128 steps).
128 steps).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...small.
-
This neglects to mention the
error of the resolvent itself, which depends on
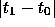 . However,
the resolvent error doesn't seem to matter much in comparison to the
error introduced by the size of the perturbation
. However,
the resolvent error doesn't seem to matter much in comparison to the
error introduced by the size of the perturbation 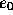 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...errors
- The error in the error, so to speak.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...recomputed.
- It is interesting to note in passing that the larger the shadow steps,
the more obvious it is that refinement converges to a solution of the
accurate integrator, not to a true solution. For, if the shadow step
errors were small enough, and the machine precision allowed it, we would be
able to ``shadow'' an entire noisy orbit using a single huge shadow step.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...procedure.
- More iterations, but each iteration takes less time. There is clearly
a trade-off here that is probably problem dependent.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...result.
-
This is probably because it did too much work in the less accurate
case, so that the solution it computed had at least 2 more accurate
digits than were requested. Then, in the more accurate case, it
managed somehow to more accurately judge its errors, and avoided
extra work.
A difference of
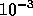 is less likely to cause this to happen.
is less likely to cause this to happen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...Insertion
-
``But the one thing we should absolutely never do is to ignore or renounce the
observational facts because we cannot explain them.''
- Halton Arp
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(0,1).
- Astronomers will note that this
does not correspond to any realistic astronomical system; however, it seems unlikely
that the precise particle distribution will effect shadowing results. This
is supported by the close correspondence of my results with those of QT,
even though they used a more realistic ``Plummer'' distribution.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...spots.
- If the orbit has a trouble spot, then
Constant Resolvent and Re-use RUS from previous successful
shadow will have no effect,
because the RUS will be re-computed in an attempt to find a shadow.
The other optimizations - Cheaper Accurate Integrator,
Large Shadow Steps, and Backwards Resolvent by Inverting Forward
Resolvent - still offer significant performance improvement.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...spots.
- Although I have never seen a clear definition of ``trouble spot'', it
seems that other practitioners of shadowing, eg., GHYS and QT, use the
term to refer to any trajectory on which refinement encounters a point
on the trajectory where the 1-step errors do not decrease with refinement,
although they do remain small and bounded.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...up.
- Although it
is completely by chance that it took exactly the same time to 3 digits.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...0..S
- 0..S means the orbit from the beginning
of shadow step 0 to the end of shadow step S.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...process
- See the discussion on stellar kinematics in
[25], particularly pages 431-438.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...encounters.
- There is some disagreement that these two factors exist. There seems to
be an ongoing debate between Kandrup and Smith
[19, 20, 21], who argue that
the growth of errors is due both to the global potential and to collisional
effects, while Goodman,
Heggie, and Hut [10] argue that collisional
encounters are the only process for the magnification of errors.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...shadow.
- Think of it like this:
F is produced by perturbing
m's orbit to have small 1-step errors under the influence of
some arbitrary, mysterious, external forces produced from a potential
that is a function only of time.
This potential comes from the other
particles, each of whom moves as if it was sliding along
a rigid, massless wire winding through space. The
motion of each particle along its wire - its motion in C -
is a function of time, and only time.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...valid.
- Note that the measure of 1-step error,
and thus the measure of a quality of any refinement procedure, is still
the full phase-space 1-step error, which is cheap to compute. In this
case, the savings per refinement is that we need to compute M
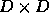 resolvents per timestep, rather than one
resolvents per timestep, rather than one 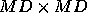 resolvent.
resolvent.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...is.
- This idea, and the next,
on related areas, are based on ideas from Scott Tremaine.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...researchers.
- Note, however, that the
practicality of attempting to integrate the solar system back several
billion years seems dubious. For, if it is already known that
the system is chaotic, then there are an almost unlimited number of
small perturbations that we cannot know about - small undiscovered
comets, or comets that passed through our system once from deep space
billions of years ago, which we cannot possibly account for; or stars
in our galaxy that perturbed the planets over the past few billion
years.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
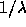 , where
, where 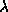 is the Lyapunov exponent.
is the Lyapunov exponent.
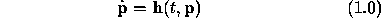
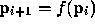 is the solution of equation 1.0 using
is the solution of equation 1.0 using 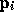 as the initial condition and integrating h to time
i+1. Then
as the initial condition and integrating h to time
i+1. Then 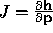 is the Jacobian of equation
1.0. The Jacobian measures how
is the Jacobian of equation
1.0. The Jacobian measures how 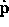 changes if
changes if
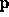 is changed by a small amount. The resolvent
is changed by a small amount. The resolvent 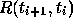 is the integral
of J(t) along the path
is the integral
of J(t) along the path 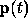 , and tells us how a small perturbation
, and tells us how a small perturbation
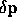 from
from 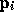 at time
at time 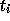 gets mapped to a perturbation from
gets mapped to a perturbation from
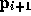 at timestep
at timestep 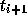 . That is,
. That is, 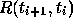 is the solution of the so-called variational equation
is the solution of the so-called variational equation
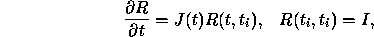
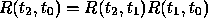 , and so a perturbation
, and so a perturbation
 at time
at time 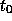 gets mapped to a perturbation
at time
gets mapped to a perturbation
at time 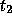 by the
matrix-matrix and matrix-vector multiplication
by the
matrix-matrix and matrix-vector multiplication
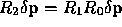 .) Finally, the linear map
in the GHYS refinement procedure is
.) Finally, the linear map
in the GHYS refinement procedure is 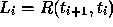 [13].
[13].
 -shadows a noisy orbit, we can find infinitely many
other true orbits nearby that also
-shadows a noisy orbit, we can find infinitely many
other true orbits nearby that also  -shadow the noisy orbit.
However, it may be that all the true orbits are packed into a space
unresolved by the machine precision.
-shadow the noisy orbit.
However, it may be that all the true orbits are packed into a space
unresolved by the machine precision.
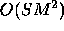 .
((25 particles
.
((25 particles 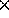 6 dimensions per particle)
6 dimensions per particle)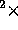 8 bytes
per double precision number
8 bytes
per double precision number 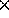 4 (2 resolvents, 2 sets of
basis vectors each covering half the space)
4 (2 resolvents, 2 sets of
basis vectors each covering half the space) 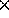 128 steps).
128 steps).
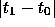 . However,
the resolvent error doesn't seem to matter much in comparison to the
error introduced by the size of the perturbation
. However,
the resolvent error doesn't seem to matter much in comparison to the
error introduced by the size of the perturbation 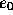 .
.
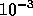 is less likely to cause this to happen.
is less likely to cause this to happen.
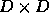 resolvents per timestep, rather than one
resolvents per timestep, rather than one 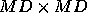 resolvent.
resolvent.