Further work on shadowing in general

 

Further work on the GHYS/QT algorithm

Here are some further ideas that I have not yet thought about in depth but should be considered. Some have already been mentioned briefly in previous chapters, but are collected here for convenience.

• An obvious item that has been overlooked is the course grained parallelism inherent in the computation of the resolvents: each resolvent is computed independently of all the others. Thus, each could be computed on a separate processer, for example using the PVM (Parallel Virtual Machinne) software package [9].
• When using constant RUS, and iterations are failing, is there some way to decide if the problem is being caused by one (or a small number) of RUS 's? If so, then only these RUS 's need be recomputed, rather than the RUS for the entire trajectory. This is potentially a large savings. An obvious possibility is that the shadow step with the greatest 1-step error (or better, the one that has the least improvement) is one that needs its RUS recomputed. Or, perhaps a shadow step with a 1-step error that refuses to decrease is too long, making the resolvent invalid. Here, the shadow step could be split into smaller segments.
• There has been much work done in numerical analysis in the area of two-point boundary value problems. Shadowing trajectories have two ends, and each end has a boundary condition: at the last point, the growth of the expanding direction is pinched; the growth of the contracting direction (expanding in negative time) is pinched at the starting point. Thus there are two points, and boundary conditions at each end. The work on two-point boundary value problems may have bearing on shadowing.
• Thus far, perturbations are allowed only in the phase-space co-ordinates of a trajectory. It seems reasonable to also allow perturbations in time. Would it help if perturbations in time were allowed as well? In other words, if the time at which the phase space point is measured is allowed to be perturbed by small amounts, will shadowing be any more successful?
• It has been repeatedly stated that the GHYS refinement procedure is similar to a Newton's method. It has many similarities: the resolvent is a Jacobian; the method is iterative; when the Jacobian is recomputed at each step, there is geometric converge; and finally, it shows some of the same weaknesses as Newton's method. Is it possible that the GHYS procedure is a Newton's method in disguise, with boundary conditions? If it can be arranged to look exactly like a Newton's method, then the massive amount of literature and code devoted to Newton's method may be brought to bear on the problem.

The Newton's method item can be formalized a bit more. In general, a one-dimensional Newton's method trying to find a zero of the equation y=f(x), given an initial guess , is usually written as . In the refinement problem, the function being computed and for which we are trying to find a zero is the function that computes the 1-step errors along the entire trajectory. Let the entire trajectory be

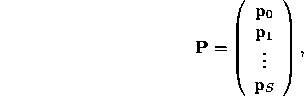
Recall the equation for the 1-step errors is

where is the function that maps point at time to the true solution at time by integrating the solution of the ODE forwards in time. In the formulation I have in mind, we also need the backward errors as defined in the SLES refinement algorithm:

where integrates the ODE backwards in time. Then, I define a new type of 1-step error, called the total 1-step error as the sum of the forward and backwards 1-step errors:

with . Let the function that computes all the 1-step errors be

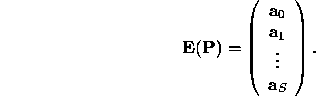
Let be the initial noisy orbit; will represent the k iteration of the Newton's method. Then the Newton's method for the GHYS refinement procedure may be written as

where is the Jacobian of the 1-step error function , i.e.,  the derivative of the 1-step errors with respect to the phase-space orbit. Writing out explicitly,

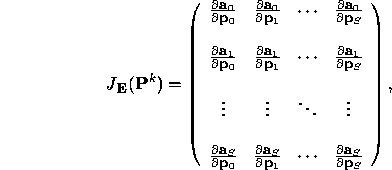
Taking partial derivatives, we see that

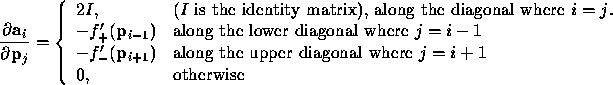
Finally, note that , and , the resolvents that we already compute.

Somewhere here is where the boundary conditions will need to come into play: if the number of phase space dimensions is 2D (each of the and vectors has 2D dimensions), then there are D boundary conditions at each end of the trajectory, limiting the growth of the stable and unstable components at their respective endpoints. The corrections (computed from ) will probably also need to be computed in a special order, as they are in the GHYS procedure. I do not currently know how to include these boundary conditions in the problem, but assuming they can be, the Newton iteration may look like the scheme described above.

More rigourous algorithms

Containment

Recall that GHYS intended refinement simply as a method to reduce noise in a trajectory, to give the more rigourous process of containment a better chance to establish rigourous proof of the existence of a true shadow. Clearly, one avenue of research is to generalize containment to work on arbitrary Hamiltonian systems. It may even prove to be about as efficient, practically speaking, as refining to machine epsilon; and most important, it is rigourous.

Uniqueness of the shadow

One interesting question, although it is not crucial to the proof of existence of shadows, is the question of uniqueness of shadows. It is already known that if one shadow exists, then infinitely many of them exist, all packed into a small volume of phase space. However, does choosing boundary conditions for and give a unique true shadow from among the infinite number of true shadows that exist, if one exists at all? It seems to me that fixing the conditions probably produces a unique shadow, because the number of boundary conditions is exactly equal to the number of degrees of freedom. For example, fixing the position and velocity at any given time produces a unique true solution, so it seems reasonable to expect that fixing half the co-ordinates at one time a and half at another time b would produce a unique solution (if one exists at all), as long as the image at time b of the initial-condition-subspace at time a is linearly independent from the final-condition-subspace at time b. It could also be tested numerically by trying slightly different first guesses for the shadow before refinement starts, or possibly by using a different ``accurate'' integrator to find the shadow. However, there may exist pathological boundary cases for which the solution is not unique.

Access count (updated once a day) since 1 Jan 1997: 9569