We should develop a better understanding of precisely what makes a direction stable or unstable. When a moving particle passes close to a fixed particle, do any of the 3 stable and 3 unstable directions lie along any of the obvious directions defined by the encounter? For example, along the path? Perpendicular to the path in the plane of the orbit? Perpendicular to the plane of the orbit? Figure 4.0 shows some possibilities.
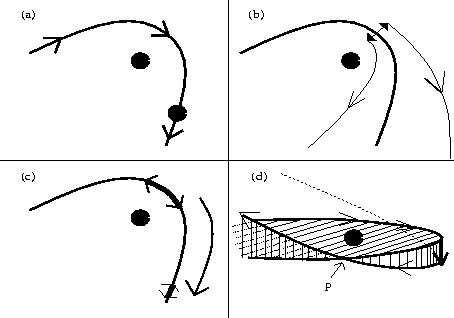
Figure 4.0: Schematic diagrams of which directions may be stable and unstable
in a close encounter of a moving particle and a fixed particle. All
perturbations happen at the point of closest approach.
(a) Schematic diagram of a close encounter, with the plane of
the orbit in the plane of the paper.
(b) If the particle's position is perturbed off the orbit,
but still in the plane
of the orbit, the particle will diverge from it's original orbit, although
not exponentially. Thus an unstable direction at the point of closest
approach may be along the line joining the particles.
(c) If the particle's position is perturbed along the orbit, but not
off it, the perturbation is damped as the particle's speed slows down
on the outbound path. Thus, at the point of closest approach, a stable
direction may lie along the orbit.
(d) A perturbation out of the plane of the orbit, as seen nearly edge
on; the plane of the orbit becomes tilted. We see that initially the
orbits converge, then cross at point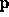 
,
then diverge from one another. We thus see
that whether a direction is ``stable'' or ``unstable'' may depend on
the duration that the variational equations are integrated. A resolvent
from the point of closest approach to
may label as ``stable'' this perturbation direction; a
resolvent that goes beyond 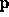may label this direction as ``unstable''.
It would be relatively easy to compute and output the dot product of the stable and unstable vectors with these special directions during a collision, but an even better understanding could be had by graphical visualization. What I have in mind is a ``roller coaster'' ride on the moving particle of an M=1 system as it moves throughout the system. Along with the view from the particle, the vectors of the stable and unstable subspaces could be rendered on screen, changing dynamically as the particle moves throughout the system.
To my knowledge, all large astrophysical N-body shadowing experiments and analyses have focused on collisional spherical systems; none have focused on disk-like or collisionless systems, such as a cold disk. Cold disks may be an ideal testing ground for shadowing of N-body systems where collisionality effects are minimized.
Definitions: A global orbit is a trajectory comprising the entire set of phase space co-ordinates of the system as a whole. A local orbit is a subset of the phase space dimensions of the global orbit that follows one individual particle. The terms global noisy orbit, local noisy orbit, global shadow orbit, and local shadow orbit are the obvious extensions of these terms. A local glitch occurs when one particle diverges from all possible shadows.
What is the effect on the system, as a whole, if two particles suffer a close encounter between each other that causes them to diverge from all possible shadows? Do the dimensions act mostly alone, suffering local glitches in small sets, or is there significant interaction between dimensions? Are other particles affected almost immediately, resulting in a ``cascade of local glitches'', or does each particle's orbit diverge independently, largely unaffected by other local glitches?
In a realistic model in which all particles move under
their mutual gravitational influence, a useful measure of error may be
the number of particles that are still locally shadowable. In other words, the
high-dimensional phase-space shadow consists of individual paths for
each particle; when one particle undergoes a local glitch and starts to
diverge from all possible shadows, the remainder of the particles may
not be affected by this for a long time. If the number of particles
that undergo local glitches increases only slowly, then the simulation still
has a reasonable amount of validity until some appreciable fraction of
the particles have diverged from their local shadows. The fact that the
high-dimensional phase-space orbit, as a whole, diverges from the global
shadow at the point of the first local glitch may be too stringent an error
criterion for large N-body shadowing. This also leads to the
question of what I call local glitch propagation:
how does the local glitch
of one particle effect the others? Clearly, a particle that diverges
from its shadow will start to effect nearby particles, eventually
participating in different collisions than would occur in any shadow.
How fast do these effects propagate throughout the system? Does the
number of new local glitches introduced during a small time interval depend
on the number of local glitches already present (leading to an exponential
growth via the familiar first-order ODE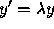 
),
or do most local glitches arise independently of one another (giving
a linear growth rate y'=c)?
Can the two be combined as simply as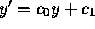 
?
If the system is softened, what does the divergence of one particle's
noisy orbit from all possible shadows imply about the validity of the
distribution of particles? If the distribution is still valid, then
the simulation is still valid under
error measure 4
from chapter 
,
even if no shadow exists.
Practically speaking, if one is using a refinement algorithm to shadow the system, the question arises of how a high-dimensional phase space trajectory should be shadowed when some of its dimensions have undergone local glitches. Those dimensions are now invalid in some sense. Should they simply be ignored for the purposes of the computation of 1-step errors? They cannot be ignored completely, or else the shadowing model will not model glitch propagation, if present. This leads naturally to the idea of what I call Fixed Motion Shadowing.
Shadowing of particular particles in large fixed-motion N-body systems, or simply Fixed Motion Shadowing, is more general than the form of shadowing done by Quinlan and Tremaine (QT) [29]. In their system, one particle moves amongst many particles whose positions are fixed. A more realistic system may be to run a standard large N-body simulation with all N particles moving for some large N, and then fix the motion of all particles in the simulation except one. This one particle's orbit is then refined in an attempt to decrease its 1-step errors under the influence of the gravitational forces of all the other particles, whose motions remain fixed to their orbits in the original noisy simulation. These particles are said to have fixed motion, while the individual particle that is shadowed is said to have moving motion, and a shadow so constructed for this particle is called a fixed motion shadow. Note that we would need to use interpolation to produce the positions of the fixed motion particles between their noisy timesteps.
The meaning of this shadowing technique is as follows.
Let the ``moving motion'' particle be called m.
Let the computed global noisy orbit be C.
Observe that, if m's 1-step errors can be reduced to zero in a fixed-motion
system, then m's local noisy orbit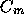 
is close to
an exact orbit under the influence of the noisy positions of
the other particles. In other words,
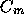is close to a true trajectory F that feels its forces from the
noisy
positions of all the fixed-motion particles -- their motions in
C. F is the fixed motion shadow.
This scheme certainly seems more realistic than a QT-like system. The existence of a fixed motion shadow seems consistent with the existence of a global shadow, for if a global shadow exists then each particle's local noisy orbit, and in particular that of the moving motion one, must closely follow its local shadow, and the fixed motion shadow will probably follow the local shadow more closely than does the local noisy orbit.
Does the existence of a fixed motion shadow F for m imply the existence of a global shadow G of comparable length? Probably not in general, because any local glitch of a particle other than m will go undetected, since that particle's motion is fixed. A fixed motion shadow probably provides a statistic similar to the ``average shadow length for an individual particle'' in conjecture 1. This in turn may provide an estimate of the ``how many particles are still shadowable'' error measure discussed in the previous section.
On the other hand, if a global shadow does exist, and if a fixed motion
shadow follows the local shadow more closely than does the local noisy
orbit, then fixed motion shadowing may provide an efficient method to
refine the orbit of a high-dimensional trajectory, by allowing refinement
of each local orbit individually in time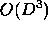 
where D is the number
of phase space dimensions per particle (six for N-body systems).
Thus numerical shadowing of
the entire phase space would take time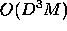 
per refinement
rather than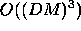 
. The question now is, how many refinements will
be needed? This method is analogous to a Gauss-Seidel method for
the solution of the matrix equation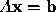 
. There may be
interplay between local orbits so that refinement of orbit j
changes orbit i<j in a way inconsistent with the local correction that
was applied to orbit i, even though at the time orbit i was refined,
the equation used was valid.
Of course, this will not help if the number of refinements required
increases, for example, as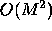 
.
If there is no glitch propagation, then each particle encounters
local glitches independent of all the others, and so the existence
of a fixed motion shadow implies nothing about the existence of
a global shadow. I expect that glitch propagation has
significant influence in collisional systems, although it probably has
little influence in collisionless systems.
A collisionless medium controls the motion of its constituent particles
via global potential effects, not local collisional effects. So in
a collisionless system, perhaps
it is possible for other particles to have different motions,
but in the same general distribution, and still result in the chosen
particle m having the same motion. For collisionless systems, we
are again led to error measure 4 from
Chapter .
To attempt the measurement of glitch propagation effects, we could allow M individual particles to have moving motion amongst N fixed-motion particles. Then, when a moving motion particle's trajectory encounters a local glitch, we would note the time, and then transfer that particle to the fixed motion group, giving it its original noisy motion, leaving M-1 particles with moving motion. This would continue until all particles have been transferred to the fixed motion group. We could then try the same experiment, except rather than transfering glitched particles to the fixed motion group with their original noisy motion, we could transfer them to the fixed motion group with the new motion computed from the more accurate trajectory at the time of the local glitch. This may help us compare glitch propagation effects between the noisy trajectory, and a trajectory with the glitched particles ``corrected'', which we assume is closer to a global shadow of the system.
If we can discover more rigourously what kinds of particle motion cause local glitches (one criterion seems to be close encounters, or large, abrupt changes in energy), then we have a criterion for choosing which particles should belong to the moving motion group. For, if we can successfully fixed-motion shadow the particles that we suspect have the highest probability of undergoing local glitches, then we can be even more confident that a global shadow exists. This leads to the following conjecture:
Conjecture 2 If 1 particle (or M particles) can be fixed-motion shadowed for time T in a collisional system, and no other particles satisfy glitch conditions, then a global shadow exists whose length is comparable to T.
More generally, if we can show that for some subset G of all
phase-space co-ordinates P, the existence of a shadow of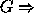 
the existence of a shadow of P, then we need only attempt shadowing of G.
This is an extremely interesting area for further work in the general
area of shadowing.
Fixed-motion shadowing could be tested against full-trajectory shadowing for at least models like those in the previous chapter in which 25 particles move. We would attempt fixed motion shadowing on 1 of the 25 particles, and see how the length of the local shadow compares with the computed global shadow.
Finally, the entire issue of fixed-motion shadowing may be moot if figure
is a correct indication of how shadowing scales
with increasing dimensions: if shadowing is as difficult in high
dimensional systems as figure suggests,
then no amount of fiddling with high dimensional kluges, like
fixed motion shadowing, will be of any use.
If shadows can be shown to exist in large collisional N-body systems, it may allow them to be simulated with simpler algorithms that ignore small perturbations that until now were thought to be important to include in models of N-body systems.
For example, Aarseth's [1] N-body integrator is a popular one for collisional systems. It includes regularization, in which close encounters between 2 particles are solved using the analytical 2-body solution with perturbations from the other particles. If a shadow can be shown to exist for such a numerical solution, it may also be possible to show that a shadow would exist if outside perturbations were ignored during 2-body close encounters. However, it's possible this may not be more efficient in the end, because the interval over which the two-body solution is valid may be smaller. Aarseth's integrator also uses individual timesteps for each particle, and interpolation of positions for particles with large timesteps when computing their forces on particles with smaller timesteps. Perhaps discrete positions could be used for particles with large timesteps, rather than their interpolated positions, and still produce shadowable solutions.
Another example of a system with perturbations is the Barnes and Hut
[3]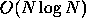 
force computation algorithm. This
algorithm produces a force function that is discontinuous in both space
and time, thus introducing artificial, relatively large perturbations;
often the force function for each particle is computed only to about
one part in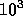 
or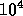 
[5].
Furthermore these kicks have been shown not to
be random, but instead have a high correlation [5].
To test whether such a system is shadowable, we
would need many moving particles (preferably thousands), and then we
should try shadowing it using the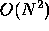 
force computation algorithm.
There has already been work to show that energy distributions are
preserved between the Barnes-Hut and 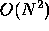algorithms
[15], but no shadowing was attempted.
More generally, we would like to study the shadowability of solution methods that introduce arbitrary ``kicks'' of various magnitudes. Roundoff and truncation error are the only kinds of kicks that have been studied in shadowing of N-body systems thus far. As seen above, there are many other types, and it is not clear which, if any, affect the robustness of shadowing results.
Thus far, not much has been said about the noisy integrator, other than that it has less accuracy than the ``accurate'' integrator. Eventually, shadowing should be attempted while using the same noisy integrator that astronomers commonly use -- often leapfrog for collisionless systems, and Aarseth's [1] for collisional systems, and usually with individual timesteps for each particle. If it turns out that long shadows do not exist for the integrators already in common use, but shadows do exist for other noisy integrators, it may be necessary for shadowing researchers to dictate to simulation researchers what integrator should be used, and at what accuracy. Comparisons should be made between symplectic vs. not and time-symmetric vs. not. In the end, the question that shadowing addresses is, How badly are we allowed to integrate?
Also, it should be noted that the leapfrog integrator should not be expected to work on non-softened collisional problems. It is an integrator that is more suited to smooth potentials.
Since time-centred
leapfrog with constant timestep is a symplectic integrator, then when
run with a suitably small timestep, it gives the exact solution to
some Hamiltonian system, although we do not know exactly what
system it is. Therefore, if we were to choose some timestep h, then
the solution we get can be considered to be a noisy solution to
the exact Hamiltonian system that is solved with the same equations
integrated with a timestep of h/2. Thus, we may be
able to learn something about Hamiltonian shadowing in general by
studying a simple system with the leapfrog integrator, or
any symplectic integrator.
Refinement is an iterative process that attempts to find a true solution close to a computed solution; it is not known in advance if such a true solution exists or what its initial conditions will be.
What if we have a specific set of initial conditions for which we
want to compute the true solution, assuming we don't mind that
the solution method may take much more computational effort than traditional
solution methods, and assuming we know a solution exists and satisfies
certain conditions?
Is it possible to develop an iterative method,
analogous to refinement in a shadowing context, that can reduce the
1-step errors towards a particular solution? Waveform
relaxation and defect correction methods both generate better and
better approximations to a solution of an initial value problem, but
can they be applied to chaotic systems? Could such
iterative methods take advantage of knowledge of the stable and
unstable subspaces by focusing effort onto the unstable subspace
in forward time and the stable subspace in reverse time? Or possibly
by using the unstable and stable vectors as basis vectors for
all computation, rather than the standard Euclidean orthonormal system?
If so, such a solution method would be valuable, for example, to
long-term solar system researchers.
If it turns out that shadowing is too stringent an error measure
for large N-body systems, we may need to resort to error measure 4 from
Chapter .
To show that the distribution of particles evolves independent of the paths of individual particles, and evolves similarly for equivalent input distributions, we could attempt many simulations whose initial conditions are all drawn randomly from the same initial distribution. For example, we could start with a distribution that ``looks'' like a specific spiral galaxy, and see if a low-resolution, smoothed animation looks the same regardless of the initial positions of the particles, as long as the initial distribution looks the same at low resolution.
If this fails, then we can try the same experiment using
error measure 5
from Chapter . If this fails, then I don't know
how to measure the reliability of N-body simulations.