When employing any particular method to study the reliability of large N-body simulations, it is essential that the method follow the N-body system for a typical duration that an astronomer is likely to simulate the system. Thus the short simulations in the previous chapter tabulating speedups for simulations lasting one crossing time, though good enough for measuring speedups, are not appropriate for studying the reliability of long running large N-body simulations. Although the number of large N-body systems that I have studied is still small, some interesting trends have already been seen.
The shadowing attempts documented in this chapter were produced in the same fashion as the previous chapter, except that longer shadowing times were attempted, up to a maximum of 256 shadow steps (25.6 standard Heggie and Mathieu time units). Shadowing was attempted first on 1 shadow-step, then doubling the number of steps until two successive failures occured on noisy orbits 2S and 4S steps long, where S was the longest shadow that was successfully constructed. In all the simulations, the total number of particles was held at N=100, while the number of moving particles M was varied from 1 to 25; N-M particles remained fixed.
Figure 3.0 plots the longest shadows found in the above systems as a function of M. The number samples per value of M was 10 for all except M equal to 1,3, and 5, which had 50, 22, and 13 samples, respectively. Although the sample sizes are small and there is much noise in this graph, it clearly shows that the length of the longest shadow that could be found, using the algorithms in this thesis, decreases with increasing M.
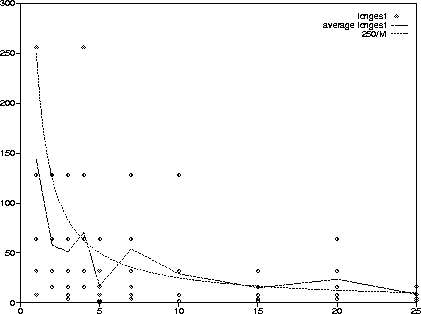
Figure 3.0: Longest shadows found in unsoftened systems of N=100 particles,
as a function of the number of moving particles M,
while N-M of the particles remain fixed.
The vertical axis measures shadow steps, which were each 0.1 standard time units.
Each diamond represents the longest shadow found for a particular orbit.
The piecewise-linear line links the averages of these systems for each M.
For comparison, the curve 250/M is also plotted.
These shadowing attempts find the glitch position to within a factor of 2. The amount of noise in this graph could be decreased significantly by attempting more accurately to pinpoint the timestep of a glitch.
Although this result does not look promising for N-body simulations, there are a number of things to keep in mind. First, it is not clear that allowing M>1 particles to move amongst N>M particles is significantly more realistic, in comparison to real systems, than having only 1 particle moving, unless M>>1. This is because as long as M<<N, each moving particle acts independently of the other moving particles. Until the number of moving particles is comparable to the number of fixed ones, the moving particles will still encounter fixed ones more often than their moving counterparts. It is not clear that 25 out of 100 is many enough moving particles.
Second, perhaps the method used to scale this problem is not realistic. Perhaps a more realistic scaling of the problem, at least from the astronomer's point of view, would be to have M particles move amongst 100M fixed ones. This would smoothen the gravitational potential, which we know from other studies [21, 10] decreases the Lyapunov exponent, and thus may lengthen the average shadow length.
Despite the above caveats, there is reason to believe that high-dimensional shadowing may be difficult. Dawsen et al. [8] show that shadowing becomes extremely difficult in systems where a Lyapunov exponent fluctuates about zero. They claim that such fluctuating Lyapunov exponents occur frequently in high-dimensional systems. I do not believe the Dawson result applies to Hamiltonian systems, because it can be shown that the number of positive eigenvalues in a Hamiltonian system is always equal to the number of negative ones.
However, I think there is another reason that
high-dimensional shadowing of large N-body systems may be difficult.
Assume that, for a fixed noise amplitude,
there exists a mean shadow length L for a QT-like system
of 1 particle moving amongst N >> 1 fixed ones. (It is possible that
no such mean exists, if the scatter in shadow lengths is great
enough.) Then, in a system in which M>1, M << N particles move,
each moving particle will encounter fixed particles far more often than
it encounters other moving particles. Thus each particle, if followed
individually, will have a mean shadow length comparable to L. Since
work in this thesis and previous work has shown that glitches seem to
occur most often near close encounters, and since close encounters occur
as a stochastic process
, a shadow length of L is
equivalent to a mean glitch rate of 1/L -- i.e., a
particle encounters glitches at a rate of 1/L per unit time. Thus,
the system of M moving particles, as a whole, encounters glitches at
a rate M/L per unit time, thus resulting in shadow lengths proportional
to L/M. As M becomes large enough to become
comparable to N, the rate that moving particles encounter other
moving particles increases, perhaps offsetting the fact that each encounter
lasts a shorter period of time. This leads to the following conjecture:
Conjecture 1 If a chaotic system with D dimensions has an average shadow length of T time units, then the equivalent system scaled appropriately to MD dimensions will have an average shadow length of T/M time units, if everything else is held constant. (Especially the integration accuracy.) In other words, shadow length is inversely proportional to dimensionality.
The graph in Figure 3.0 seems consistent with this conjecture, as the curve 250/M indicates.