The general astrophysical N-body system consists of N particles
moving according to Newton's three laws of motion, with Newton's familiar
gravitational law 
being the only source of force.
Let 
be the unit vectors of the standard
Cartesian (x,y,z) system.
Let 
be
the position vector of particle i.
Let 
be
the vector pointing from particle i to particle j, i.e.,
the position of particle j with respect to particle i.
Thus
The force that particle j exerts on particle i is
where G is the gravitational constant, 
are the masses of
the particles, 
is the vector pointing from particle i to
particle j, 
is the magnitude of this vector, and 
is the unit vector pointing in the direction of .
Let the total force on particle i be 
. It is the sum of all the
forces from all the other particles.
Thus the total force on particle i is
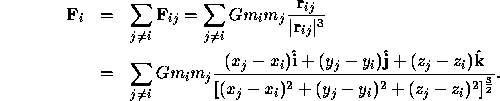
For a 3-dimensional space, this is a set of 3N second-order
ordinary differential equations (ODEs), which we translate into a set of
6N first-order ODEs by letting the velocity
and then building
the phase-space vector of the entire system as
.
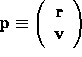Thus the first-order ODE system is
where 
is the vector representing the accelerations of all the particles.
At any given time, the position 
and velocity 
of every particle
is known.
Thus 
is simply , and 
is the set of time-derivatives of the velocity 
of each particle, where
If force softening is used, the denominator instead becomes
where 
is the softening parameter.
