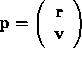 be
be 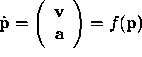 .
f has no dependence on time. The Jacobian
of f,
.
f has no dependence on time. The Jacobian
of f,
Let the function computing the derivative of 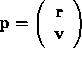 be
be 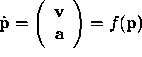 .
f has no dependence on time. The Jacobian
of f,
.
f has no dependence on time. The Jacobian
of f, ![]() is
is
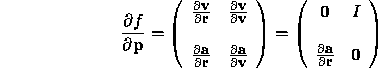
where ![]() is the 3N-square zero matrix, and I is the 3N identity
matrix. If all particles move, then the entire Jacobian is 6N square.
If only M particles move, then there is no meaning to the entries in
the Jacobian owned by particles that do not move, and so the Jacobian is
only 6M square. The only difficult part of this Jacobian is
is the 3N-square zero matrix, and I is the 3N identity
matrix. If all particles move, then the entire Jacobian is 6N square.
If only M particles move, then there is no meaning to the entries in
the Jacobian owned by particles that do not move, and so the Jacobian is
only 6M square. The only difficult part of this Jacobian is
![]() , which is a 3N-square matrix, and
, which is a 3N-square matrix, and
![]() where
where ![]() is the acceleration of particle i, given by equation
A.1,
and
is the acceleration of particle i, given by equation
A.1,
and ![]() is its position in 3-space. Thus,
is its position in 3-space. Thus,
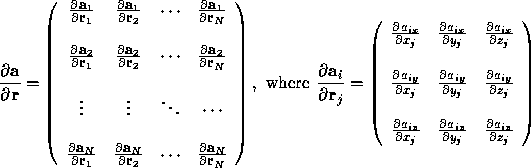
Finally, if we let ![]() represent one of
represent one of ![]() , it
can be shown that
, it
can be shown that
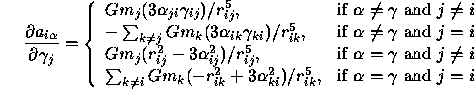
where, for example, ![]() is the
is the ![]() component of
component of ![]() .
If softening is employed, substitute
.
If softening is employed, substitute ![]() for
for ![]() and
and ![]() for
for ![]() .
.
Wayne Hayes