


Next: Optimal structure of a
Up: The problems
Previous: Minimal triangulation of a
Optimal grouping of a matrix product
A matrix is a rectangular array of numbers. The product of two
matrices, 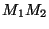 is defined, so long as
is defined, so long as 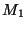 has the same number
of columns as
has the same number
of columns as 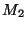 has rows. Suppose
has rows. Suppose 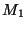 has
has 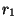 rows and
rows and 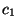 columns,
columns, 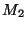 has
has 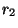 rows and
rows and 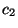 columns (
columns (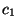 must equal
must equal
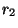 ), then the product
), then the product 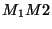 requires
requires
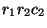 multiplications of array elements. Matrix multiplication is
associative (although not commutative), so three or more matrices can
be multiplied (so long as the appropriate adjacent dimensions match):
multiplications of array elements. Matrix multiplication is
associative (although not commutative), so three or more matrices can
be multiplied (so long as the appropriate adjacent dimensions match):
Although the value of
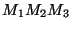 is the same whichever way you
group them, the amount of work (multiplications of array elements) is
not. For example, suppose
is the same whichever way you
group them, the amount of work (multiplications of array elements) is
not. For example, suppose 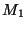 is a
is a 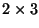 matrix (2 rows, 3
columns),
matrix (2 rows, 3
columns), 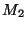 is
is 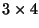 , and
, and 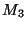 is
is 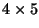 . Then the
grouping
. Then the
grouping
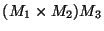 costs:
costs: 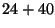
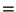
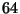 multiplications. The grouping
multiplications. The grouping
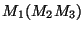 costs:
costs: 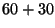
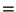
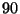 multiplications. This disparity gets worse for longer chains of
matrices. What is the best way to group
Here is a first attempt at finding a minimum-cost grouping. In
analogy with triangulation, denote the minimum cost of grouping
matrices
multiplications. This disparity gets worse for longer chains of
matrices. What is the best way to group
Here is a first attempt at finding a minimum-cost grouping. In
analogy with triangulation, denote the minimum cost of grouping
matrices
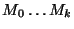 as
as ![$ c[0][k]$](img63.png) , and the product
, and the product
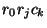 as
as 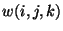 . Then for each choice of
. Then for each choice of 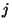 with
with
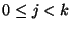 we
check the value of
we
check the value of
![$ c[0][j-1] + c[j][k] + w(i,j,k)$](img66.png) , and take the
minimum. This formula looks close to that for triangulation except
for two things: the first part of the sum is
, and take the
minimum. This formula looks close to that for triangulation except
for two things: the first part of the sum is ![$ c[0][j-1]$](img67.png) rather than
rather than
![$ c[0][j]$](img68.png) (since the matrices don't overlap), and the function
(since the matrices don't overlap), and the function
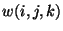 is different.
is different.
You can fix the first problem by changing notation slightly.
Define ![$ c[i][k]$](img22.png) to be the minimum cost of grouping matrices
to be the minimum cost of grouping matrices
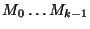 (instead of
(instead of 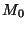
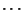
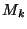 ), so
), so 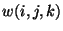
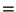
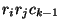 , and our recursive formula is now the same as
Equation 1, except for
, and our recursive formula is now the same as
Equation 1, except for 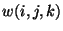 being
different (and aren't there C++ features that might help with that?).
You can use the same algorithm for both problems. The cost of a
minimal grouping of matrices
being
different (and aren't there C++ features that might help with that?).
You can use the same algorithm for both problems. The cost of a
minimal grouping of matrices 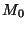
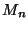 is
is ![$ c[0][n+1]$](img75.png) .
.



Next: Optimal structure of a
Up: The problems
Previous: Minimal triangulation of a
Danny Heap
2002-11-27
![]() is defined, so long as
is defined, so long as ![]() has the same number
of columns as
has the same number
of columns as ![]() has rows. Suppose
has rows. Suppose ![]() has
has ![]() rows and
rows and ![]() columns,
columns, ![]() has
has ![]() rows and
rows and ![]() columns (
columns (![]() must equal
must equal
![]() ), then the product
), then the product ![]() requires
requires
![]() multiplications of array elements. Matrix multiplication is
associative (although not commutative), so three or more matrices can
be multiplied (so long as the appropriate adjacent dimensions match):
multiplications of array elements. Matrix multiplication is
associative (although not commutative), so three or more matrices can
be multiplied (so long as the appropriate adjacent dimensions match):
![]() to be the minimum cost of grouping matrices
to be the minimum cost of grouping matrices
![]() (instead of
(instead of ![]()
![]()
![]() ), so
), so ![]()
![]()
![]() , and our recursive formula is now the same as
Equation 1, except for
, and our recursive formula is now the same as
Equation 1, except for ![]() being
different (and aren't there C++ features that might help with that?).
You can use the same algorithm for both problems. The cost of a
minimal grouping of matrices
being
different (and aren't there C++ features that might help with that?).
You can use the same algorithm for both problems. The cost of a
minimal grouping of matrices ![]()
![]()
![]() is
is ![]() .
.