


Next: Optimal grouping of a
Up: The problems
Previous: The problems
Minimal triangulation of a convex polygon
A convex polygon has interior angles that are each strictly less than
180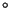 (or
(or 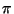 radians, if you like). A triangulation
of a convex polygon is formed by drawing diagonals between
non-adjacent vertices (corners), provided you never intersect another
diagonal (except at a vertex), until all possible choices of diagonals
have been used (see Figure 1).
radians, if you like). A triangulation
of a convex polygon is formed by drawing diagonals between
non-adjacent vertices (corners), provided you never intersect another
diagonal (except at a vertex), until all possible choices of diagonals
have been used (see Figure 1).
Figure:
Two triangulations of the same convex pentagon. The
triangulation on the left has a cost of 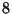
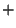
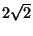
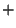
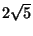 (approximately 15.30), the one on the right has a
cost of
(approximately 15.30), the one on the right has a
cost of 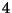
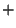
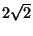
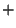
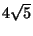 (approximately
15.77). If you index the vertices counter-clockwise from
(approximately
15.77). If you index the vertices counter-clockwise from
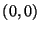 (vertex 0) to
(vertex 0) to 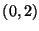 (vertex
(vertex 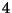 ), then you could
specify the triangulation on the left by listing the indices of
its component triangles: 0 3 4, 0 1 3, and
1 2 3. You could specify the triangulation on the
right similarly: 0 3 4, 0 2 3,
0 1 2.
), then you could
specify the triangulation on the left by listing the indices of
its component triangles: 0 3 4, 0 1 3, and
1 2 3. You could specify the triangulation on the
right similarly: 0 3 4, 0 2 3,
0 1 2.
|
|
Suppose a convex polygon has vertices 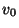 ,
, 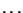 ,
, 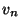 .
In any triangulation we can assign a weight to each triangle: the
length of its perimeter.2Let
.
In any triangulation we can assign a weight to each triangle: the
length of its perimeter.2Let 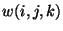 denote the length of the perimeter of
denote the length of the perimeter of
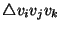 . The cost of a triangulation is just the sum of the
weights of its component triangles. We want to find a triangulation
with the minimum cost.
. The cost of a triangulation is just the sum of the
weights of its component triangles. We want to find a triangulation
with the minimum cost.
Here's a sketch of how to find a minimum cost triangulation of a
convex polygon with 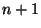 vertices:
vertices:
- Number the vertices of your polygon from 0 to
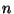 .
.
- Denote the cost of a minimal triangulation (which you haven't
yet found) of your polygon as
![$ c[0][n]$](img19.png) . Similarly, your polygon
contains sub-polygons with vertices
. Similarly, your polygon
contains sub-polygons with vertices 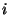 through
through 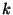 (if
(if 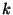 is at
least 2 greater than
is at
least 2 greater than 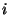 ), and you can denote the weight of a
minimal triangulation of such a sub-polygon as
), and you can denote the weight of a
minimal triangulation of such a sub-polygon as ![$ c[i][k]$](img22.png) .
.
- Possible values of
![$ c[i][k]$](img22.png) fall into two cases. Case
one: if
fall into two cases. Case
one: if 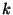
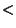
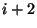 then the polygon with vertices
then the polygon with vertices 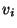
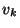 has fewer than 3 vertices, and no triangulation is possible, so
an appropriate minimum triangulation cost is 0. Case two: if
has fewer than 3 vertices, and no triangulation is possible, so
an appropriate minimum triangulation cost is 0. Case two: if
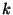
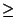
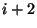 , then there are one or more choices of
, then there are one or more choices of 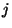 where
where 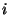
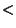
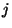
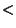
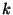 . For each choice of
. For each choice of 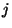 , calculate
, calculate ![$ c[i][j]$](img29.png)
![$ c[j][k]$](img2.gif)
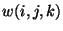 -- the minimum over all appropriate
-- the minimum over all appropriate 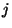 is
is
![$ c[i][k]$](img22.png) . These two cases give the following recursive formula:
. These two cases give the following recursive formula:
![$\displaystyle c[i][k] = \begin{cases}0 & k < i + 2 \min_{i < j < k} \{c[i][j] + c[j][k] + w(i,j,k)\} & \text{otherwise} \end{cases}$](img3.gif) |
(1) |
Record which index 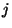 corresponds to the minimum (you might denote it
corresponds to the minimum (you might denote it
![$ m[i][k]$](img32.png) ).
).
- Suppose
![$ m[0][n]$](img33.png) is denoted
is denoted 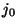 , then you know that
, then you know that
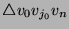 is part of a minimal
triangulation. You can find more triangles in this minimal
triangulation using
is part of a minimal
triangulation. You can find more triangles in this minimal
triangulation using ![$ m[0][j_0]$](img36.png) and
and ![$ m[j_0][n]$](img37.png) . Continue until
you've found all triangles in a minimal triangulation.
. Continue until
you've found all triangles in a minimal triangulation.
Although it is possible to build up a table of values ![$ c[i][k]$](img22.png) iteratively (as described in your course notes), for this assignment
you must find
iteratively (as described in your course notes), for this assignment
you must find ![$ c[0][n]$](img19.png) recursively, using memoization (mentioned
in lecture) to prevent redundant calculations of the same
value.
recursively, using memoization (mentioned
in lecture) to prevent redundant calculations of the same
value.



Next: Optimal grouping of a
Up: The problems
Previous: The problems
Danny Heap
2002-11-27
![]() (or
(or ![]() radians, if you like). A triangulation
of a convex polygon is formed by drawing diagonals between
non-adjacent vertices (corners), provided you never intersect another
diagonal (except at a vertex), until all possible choices of diagonals
have been used (see Figure 1).
radians, if you like). A triangulation
of a convex polygon is formed by drawing diagonals between
non-adjacent vertices (corners), provided you never intersect another
diagonal (except at a vertex), until all possible choices of diagonals
have been used (see Figure 1).
![\resizebox{0.7\textwidth}{!}{
\includegraphics[0pt,0pt][320pt,145pt]{triangulation.eps}}](img11.png)
![]() ,
, ![]() ,
, ![]() .
In any triangulation we can assign a weight to each triangle: the
length of its perimeter.2Let
.
In any triangulation we can assign a weight to each triangle: the
length of its perimeter.2Let ![]() denote the length of the perimeter of
denote the length of the perimeter of
![]() . The cost of a triangulation is just the sum of the
weights of its component triangles. We want to find a triangulation
with the minimum cost.
. The cost of a triangulation is just the sum of the
weights of its component triangles. We want to find a triangulation
with the minimum cost.
![]() vertices:
vertices:
![]() iteratively (as described in your course notes), for this assignment
you must find
iteratively (as described in your course notes), for this assignment
you must find ![]() recursively, using memoization (mentioned
in lecture) to prevent redundant calculations of the same
value.
recursively, using memoization (mentioned
in lecture) to prevent redundant calculations of the same
value.