Problem Set 9
DFAs
1 Closure
1.1
Let \(A\), \(B\) be regular languages. Show that \(A \cap B\) is also regular.
Solution
By De Morgan’s Law, we know that \(\overline{A \cap B} = \overline{A} \cup \overline{B}\). Thus, \(A \cap B = \overline{\overline{A} \cup \overline{B}}\).
Since \(A\) and \(B\) are regular, and regular languages are closed under union and complement, we have \(\overline{A}\), and \(\overline{B}\) are regular. This implies \(\overline{A} \cup \overline{B}\) is regular. This implies \(\overline{\overline{A} \cup \overline{B}} = A \cap B\) is regular as required.
Alternatively, use the same construction as the one from the lecture for \(A \cup B\), the only difference is a state \((x, y)\) should be accepting if and only if \(x\) is accepting in the DFA for \(A\) and \(y\) is accepting in the DFA for \(B\).
1.2
Let \(A\), \(B\) be regular languages. Show that \(A \Delta B\) is also regular, where \(A \Delta B\) is the symmetric difference of \(A\) and \(B\).
Solution
Let \(A, B\) be regular languages. Since we’ve shown that regular languages are closed under complementation, union and intersection, \((\overline{A} \cap B) \cup (\overline{B} \cap A) = A\Delta B\) is regular.
Alternatively, use the same construction from the lecture for \(A \cup B\). The only difference is a state \((x, y)\) should be accepting if and only if \(x\) is accepting in the DFA for \(A\) if and only if \(y\) is not accepting in the DFA for \(B\).
2 DFA to Language
Determine whether or not the following are valid DFA definitions. If the DFA is valid, what is the language of the DFA?
2.1
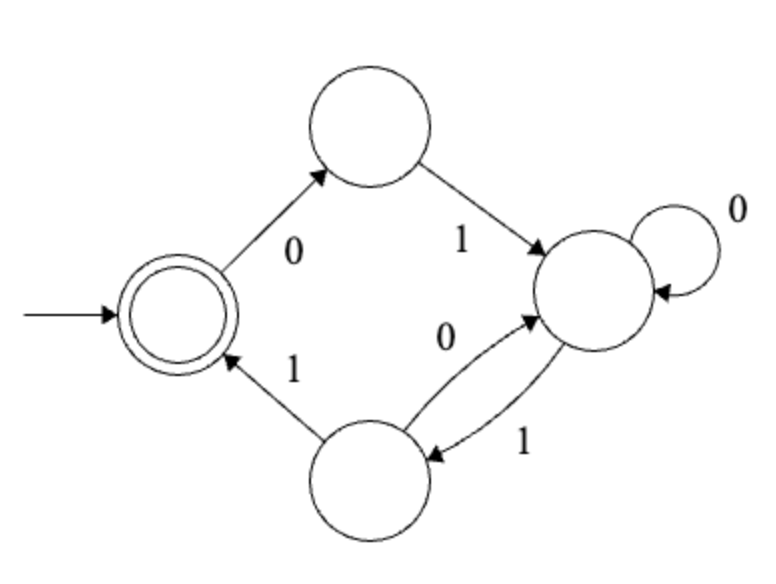
Solution
Not valid - the top state has no outgoing 0 transition.
2.2
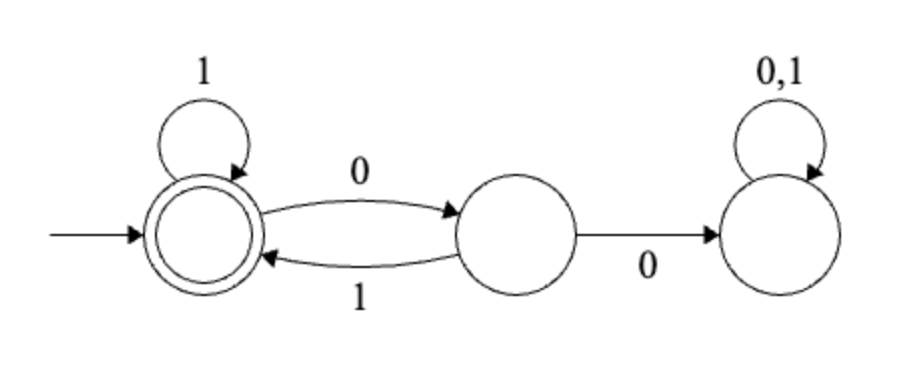
Solution
Every 0 is followed by a 1.2.3
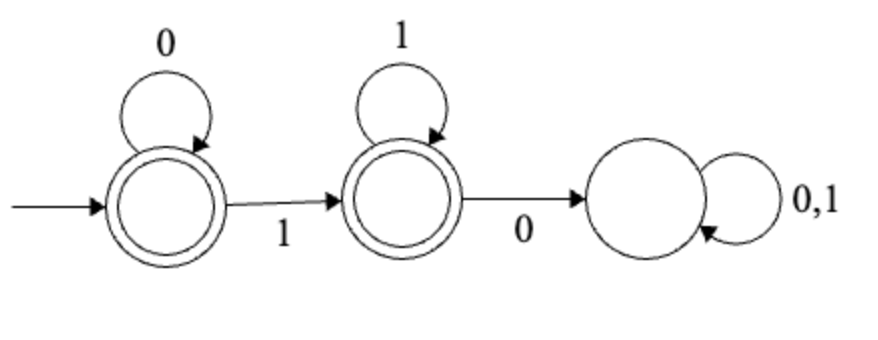
Solution
Doesn’t contain 10
3 Language to DFA
3.1
Find a DFA/NFA for the following languages:
\(L_1 = \{w \in \{0,1\}^* : w \text{ is a binary representation of a multiple of 3}\}\). Find a DFA for \(L_1\).
\(L_2 = \{w \in \{0,1\}^* : \text{every 1 is preceeded by at least two zeros }\}\).
\(L_3 = \{w \in \{0,1\}^* : \text{every 1 is preceeded by at exactly two zeros }\}\).
\(L_4 = \{w \in \{0,1\}^* : \text{every 1 is preceeded by at most two zeros }\}\).
\(L_5 = \{w \in \{0,1\}^* : \text{w contains neither 01 nor 10}\}\).