Tutorial: Induction
2025-05-21
1 Induction
1.1
\(\forall n \in \mathbb{N}, n \geq 1. (12^n - 1)\) is a multiple of 11
Solution
By induction.
Base case. For the base case, observe that \(12^1 - 1 = 11\) which is divisible by 11.
Inductive step. Let \(k \in \mathbb{N}\), be any natural number with \(k \geq 1\), and assume \(12^k - 1 = 11a\) for some \(a \in \mathbb{N}\). Then, we have
\[ \begin{align*} 12^{k+1} - 1 &= 12^k \cdot 12 - 1\\ &= (11a + 1) \cdot 12 - 1\\ &= 12\cdot 11a + 11\\ &= 11\cdot (12a + 1).\\ \end{align*} \]
Since \(a\) is a natural number so is \(12a + 1\), thus \(12^{k+1}\) is divisible by 11, completing the induction.1.2
\(\forall n \geq 4. n^4 \leq 4^n\)
Solution
By induction.
Base case. Both the RHS and the LHS are \(4^4\), so the base case holds.
Inductive step. Let \(k \in \mathbb{N}\) with \(k \geq 4\), and assume \(k^4 \leq 4^k\). We then have
\[ \begin{align*} (k + 1)^4 &= k^4 + 4k + 6k^2 + 4k^3 + 1 \\ &\leq k^4 + k^2 + 6k^2 + k^4 + k^4 & (k \geq 4, k^4 \geq 1) \\ &\leq k^4 + k^4 + k^4 + k^4 & (k^2 \geq 7, k^4 \geq k)\\ &= 4k^4\\ &\leq 44^k &(IH)\\ &= 4^{k+1}, \end{align*} \]
as required.
1.3
\(\forall n \in \mathbb{N}. \sum_{i=1}^{2^n}\frac{1}{i} \geq 1 + \frac{n}{2}\)
Solution
Base case. For the base case, the LHS and the RHS are both equal to \(1\).
Inductive step. Let \(k \in \mathbb{N}\) be any natural number and suppose \(\sum_{i=1}^{2^k}\frac{1}{i} \geq 1 + \frac{k}{2}\). Then
\[ \begin{align*} \sum_{i=1}^{2^{k+1}}\frac{1}{i} &= \sum_{i=1}^{2^k} \frac{1}{i}+ \sum_{i=2^{k} + 1}^{2^{k+1}} \frac{1}{i}\\ &\geq 1 + \frac{k}{2}+ \sum_{i=2^{k} + 1}^{2^{k+1}} \frac{1}{i}\\ &\geq 1 + \frac{k}{2}+ \sum_{i=2^{k} + 1}^{2^{k+1}} \frac{1}{2^{k+1}}\\ &= 1 + \frac{k}{2}+ \frac{2^{k}}{2^{k+1}}\\ &= 1 + \frac{k+1}{2},\\ \end{align*} \]
completing the induction.2 Triominoes
A triomino is a domino that looks like an \(L\). Below is an illustration of a triomino and what it looks like when rotated.
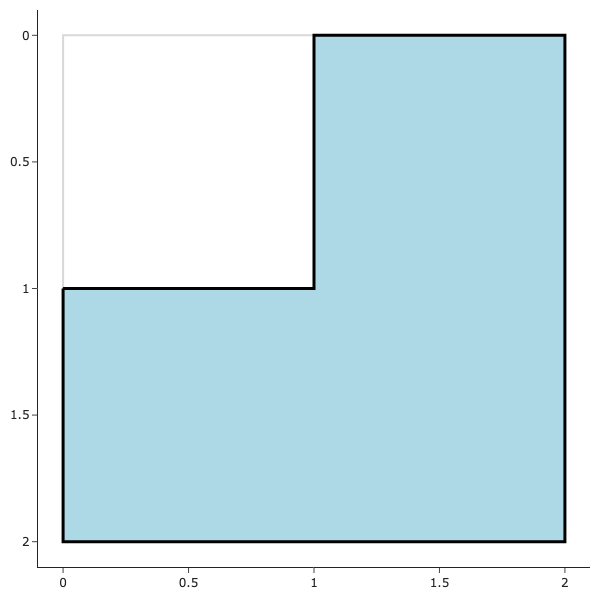
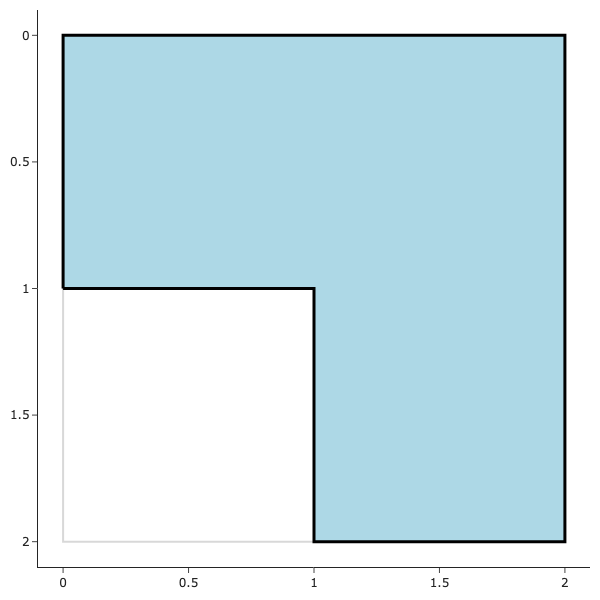
Consider a \(2^n \times 2^n\) grid with one square removed.
We want to tile the grid using triominoes. For example:
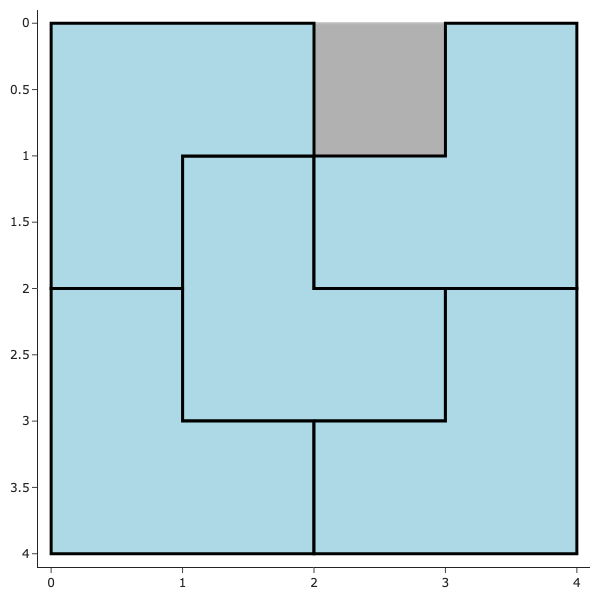
Note the gray square is the one that has been removed.
2.1
Prove for every \(n \in \mathbb{N}\), with \(n \geq 0\), you can tile any \(2^n \times 2^n\) grid with one square missing using only triominoes (you can rotate them however you wish).
Solution
Also see Logan’s Walkthrough here.
By induction.
Base case. a \(2^0\times 2^0\) grid with one square missing has no squares left to be tiled so the base case holds.
Inductive step. Let \(k \in \mathbb{N}, k \geq 0\) be any natural number at least 1, and assume the claim is true for \(2^k \times 2^k\) grids with one square removed. We now consider the \(2^{k+1} \times 2^{k+1}\) grid with one square removed. Note that this is four \(2^k \times 2^k\) grids arranged in a square. If the removed square occurs in the subgrid, we can completely tile the that subgrid by the induction hypothesis. For the remaining 3 subgrids, remove the square in the inner corner of the grid. By the induction hypothesis, these three subgrids can also be tiled using triominoes. Finally, the three squares we removed from the inner corners of the subgrids can be tiled using a single triomino.
Here is a picture: 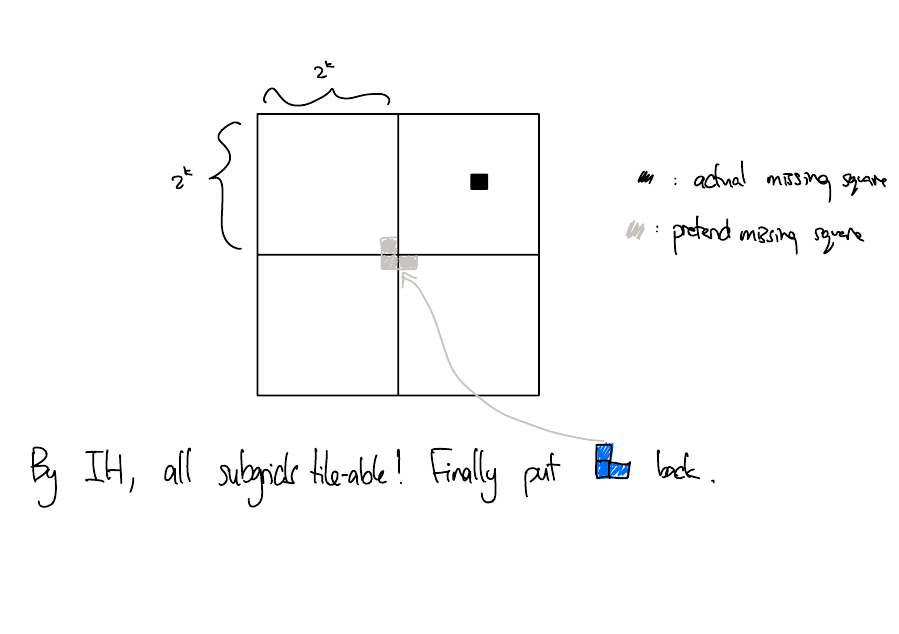
3 Induction and Recursion
There is a close relationship between inductive proofs and recursive algorithms.
Many times an inductive proof of “for all \(n\), X is possible” can be translated into a recursive algorithm that computes X for any \(n\).
For example, if you look carefully at the proof of the triominoes problem, not only does it show that a tiling \(2^k \times 2^k\) grid with one square removed using triominoes is possible, it also tells you how to do it.
3.1
Say in words how the inductive proof gives a recursive algorithm to find the tiling.
Solution
If dealing with a \(1\times 1\) grid with a missing tile, then there is nothing to do!
Find which quadrant the missing square is in. Tile that quadrant recursively. Put a triomino in the center of the grid, covering the three squares in the other quadrants. Tile the other three quadrants recursively.3.2
Tile the following grid with triominoes.
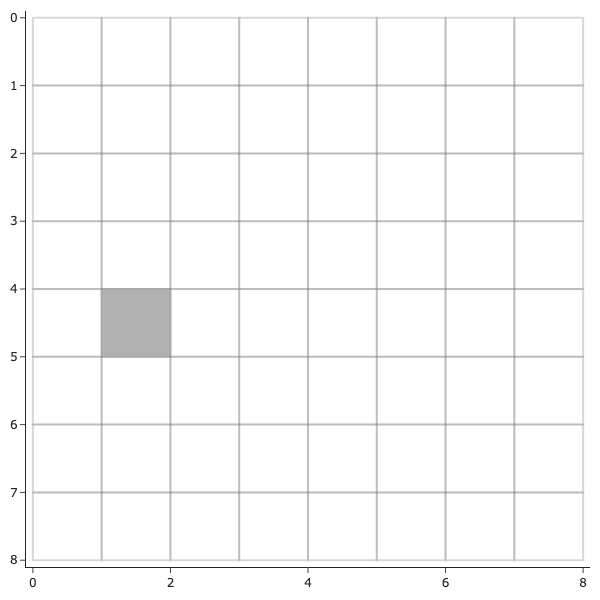
Solution
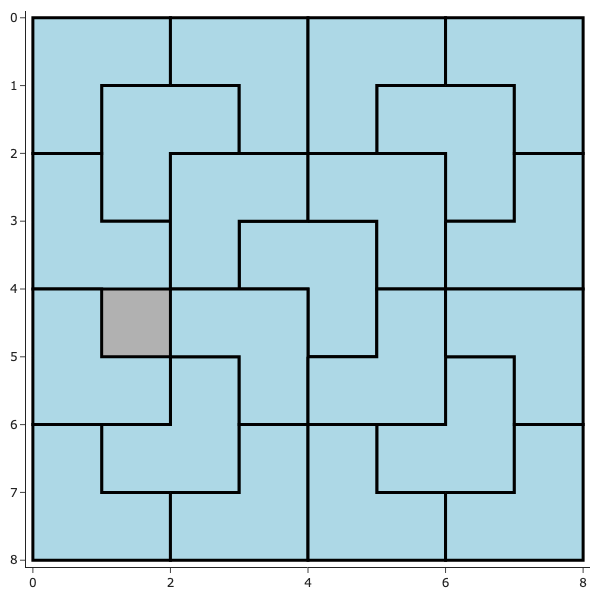
3.3
As another example, the postage stamp problem from lecture, where we proved that any postage amount \(n \geq 8\), can be made using using only 3-cent and 5-cent stamps. If you look carefully at the proof, it also tells you how to do it. In class we gave two different proofs for this fact and the two proofs give different recursive algorithm to find the stamps.
How does the first proof give a recursive algorithm to find the stamps?Solution
if \(n\) is 8, 9 or 10, and then make 8 (3 + 5), 9 (3 + 3 + 3), or 10 (5 + 5). If \(n > 10\), subtract 3 and make \(n-3\).3.4
How does the second proof give a recursive algorithm to find the stamps?
Solution
if \(n\) is 8, 9 or 10, and then make 8 (3 + 5), 9 (3 + 3 + 3), or 10 (5 + 5). To make \(n\), make \(n-1\). If the number of 5 cent stamps used to make \(n-1\) is at least one, make \(n\) by removing one 5 cent stamp and adding two 3 cent stamps. If the number of 5 cent stamps used to make \(n-1\) is 0, make \(n\) by removing three 3 cent stamps and adding two 5 cent stamps.3.5 (Optional)
Implement the algorithms for triomino tiling and postage stamp making here.