Tutorial: DFAs and NFAs

2025-05-21

1 Regular

1.1

$L_1 = \{w : w \text{ contains 000 as a substring}\}$

Solution

1.2

$L_2 = \{w : w \text{ starts and ends with 1}\}$

Solution

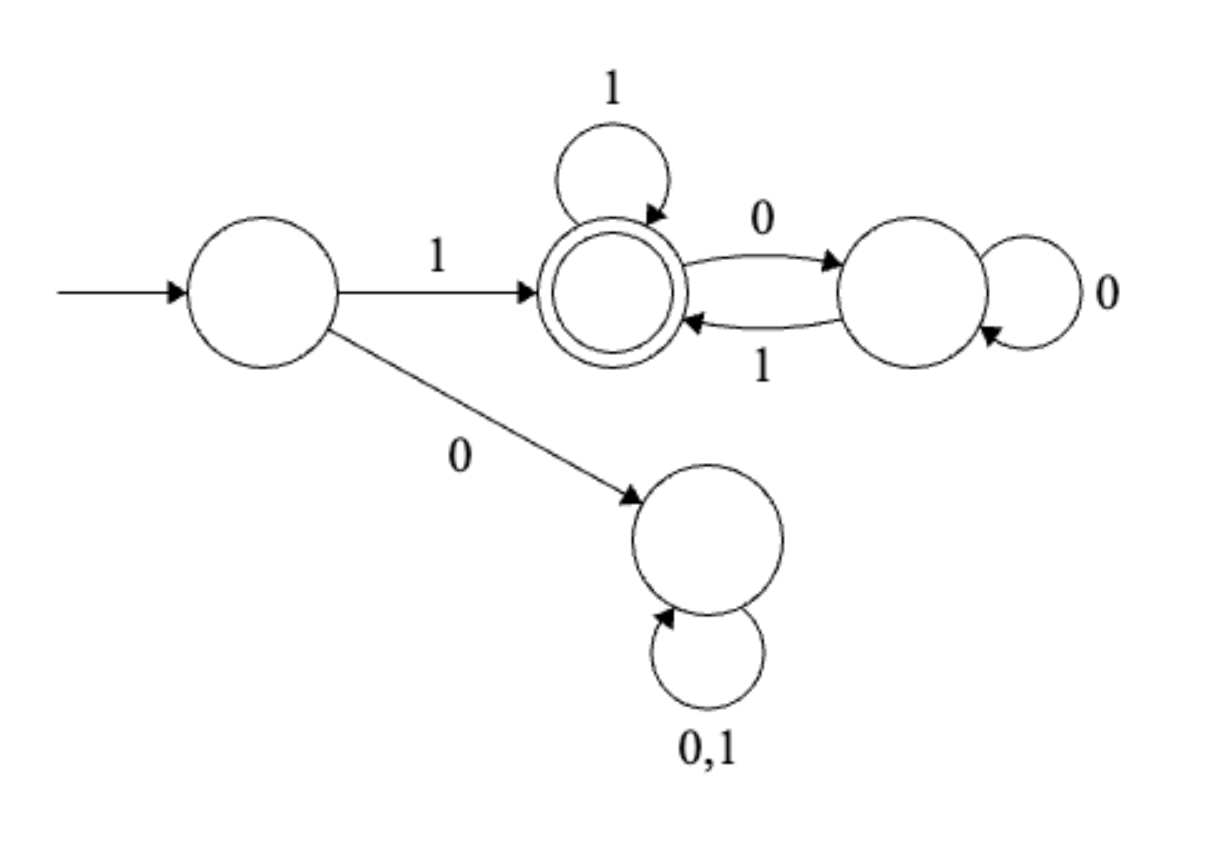
1.3

$L_3 = \left\{ w : \ \begin{array}{l} w \text{ is the binary representation of a number} \\ \text{ of the form $2^n + 1$ for some $n \in \mathbb{N}$} \end{array} \right\}$

Solution

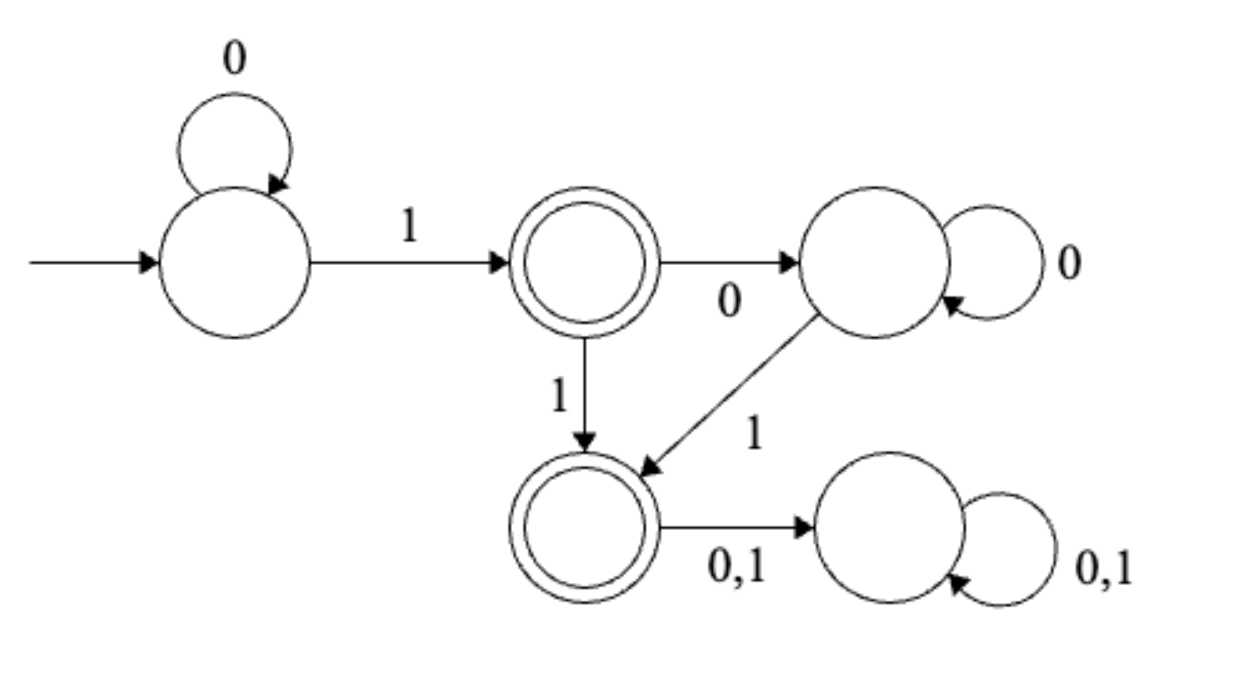
1.4

$L_4 = \left\{ w : \ \begin{array}{l} \text{the number of 1s in $w$ mod 3} \\ \text{is less than the number of 0s in $w$ mod 3} \end{array} \right\}$

Solution

2 Parallel

2.1 Parallel Construction

Let

$L_1 = \{w : w \text{ has odd length}\}$
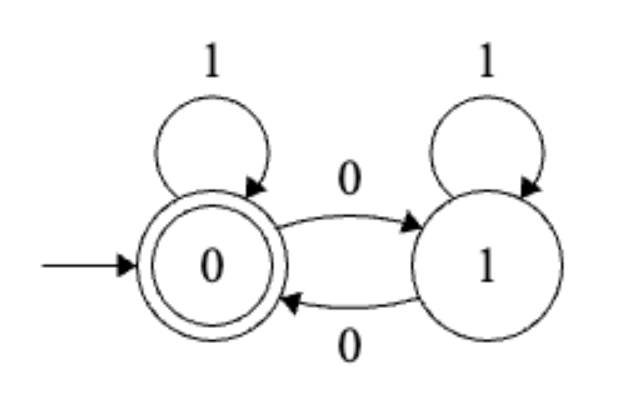
$L_2 = \{w : w \text{ has an even number of 0}s\}$

2.2

Exercise. Define DFAs for $L_1$ and $L_2$. Give a label to each state.

2.3

Exercise. Use the previous two DFAs and the ‘running in parallel’ construction to construct a DFA for $L_1 \cup L_2$.

Solution

2.4 If there’s extra time

For extra practice: find regular expressions for all the languages in this tutorial