There are 6 major optimizations that I have applied to the GHYS/QT refinement procedure. The first two are trivial, and no further details will be given about them. The final four will be explained in more detail in the remaining sections of this chapter.
Definition If program A has a speedup of 
over
program B, then the execution time of A is a fraction 
of
B's time; in other words A runs times faster than B.
QT re-computed a new resolvent for each stable and unstable vector, i.e.,
at each timestep they computed 6M resolvents.
However, a resolvent 
is a matrix operator that applies to
all small perturbations of the orbit from time 
to 
.
Thus only 2 resolvents per timestep need be computed: one for evolving
perturbations
forward in time, and another to evolve them backwards.
Since most of the time is spent computing the resolvents, fixing this
oversight provides an immediate speedup of a factor of about 3M.
The above optimization can be extended even further by
noting that the resolvent matrix 
that maps perturbations from timestep
i to i+1 is precisely the inverse matrix of the resolvent that maps
small perturbations from timestep i+1 to i. Thus, rather than doing
an integration from timestep i+1 backwards to time i to compute
, can be inverted using matrix operations, or the system
can be solved, whenever necessary, using standard elimination
schemes. This gives an
additional speedup of about 2, since only one resolvent per timestep
need explicitly be computed using integration of the variational equations.
Define a shadow step as a time interval across which the 1-step error and correction co-efficient are computed. QT used every internal timestep of their integrator's noisy orbit as a shadow step, but this is not necessary. It is reasonable to skip timesteps in the original orbit to build larger shadow steps. This means that fewer resolvents and stable/unstable directions need to be computed and stored.
When computing the resolvent and 1-step errors during early refinements,
it is not necessary to
compute them to extremely high accuracy. Since the
initial 1-step errors may have magnitudes of about 
,
the resolvents and 1-step errors need only be computed to a tolerance of,
say, 
, i.e., 3 extra digits.
QT always computed the 1-step errors and resolvents to a tolerance
of 
.
If a shadow exists, then by definition it cannot be too far
away from the original noisy orbit. It is reasonable to assume that the
resolvents, unstable and stable directions (abbreviated RUS)
will change little as the orbit is perturbed towards the shadow.
Thus, it may not be necessary to recompute the
RUS for every refinement iteration. This is probably the biggest savings,
because in combination with the cheaper integrator, it means that the
RUS usually need only be computed once to a tolerance of about , and
this RUS will suffice for all future refinements. This is analogous
to a simplified Newton's method that does not recompute the Jacobian
at ever iteration.
Recall that to find the
longest possible shadow of a noisy orbit, we attempt to shadow for longer
and longer times until shadowing fails. Assume shadowing for S shadow steps
produces a shadow A. Then attempt shadowing for S+k timesteps
for some integer k, and assume a successful shadow B will be found.
Since A and the first S steps of B both shadow the same noisy orbit,
they must be close to one another.
By the same argument as the previous paragraph, the RUS that was computed
for A
can probably be re-used for the first S shadow steps of B.
Thus only k new RUS 
's need be computed.
I use the acronym RUS to mean the set of all Resolvents,
Unstable, and Stable vectors for the entire trajectory.
The RUS at a particular timestep i is referred to as RUS .
For a smooth, continuous, well-behaved function, the Jacobian
(i.e., the derivative) is also smooth and continuous. Most Hamiltonian
systems (that I have seen) studied by scientists are at least piecewise of
this sort. The N-body problem, in particular, is of this sort, as long
as no particles pass within 0 distance of each other.
This implies that
the resolvent along a particular path will not change much if the
path is perturbed slightly.
Since the unstable and stable unit vectors are derived solely from the
resolvents, they will also change only slightly when the path is perturbed.
Thus, the RUS computed on the first
refinement iteration should be re-usable on later iterations, and
computing the new 1-step errors is the only significant work to be
performed on each new refinement iteration.
(Computing the corrections from the errors
is much less CPU intensive than computing the errors themselves.)
I have empirically found that computing the RUS to a tolerance of
between 
and 
usually suffices to refine the orbit
down to 1-step errors near the machine precision. If refinement fails
using constant RUS, then perhaps there is a spot in the orbit where
some RUS 's change quickly with small perturbations in the path. In that
case, the RUS can be re-computed for a few refinements, after which constant
RUS may be tried again. However, a case in which constant RUS fails often
suggests that there as a mild trouble spot somewhere on the orbit that
may cause a glitch in longer shadows.
The algorithm used to switch between constant RUS and recomputed RUS
uses a running-average ``memory'' scheme to keep track of the progress of
the magnitude of the maximum 1-step error over the previous few refinements.
Originally, I used a simple algorithm (like QT's) that would signal
failure when a certain number K of successive refinements had failed,
for 
and K=3. (See here for the
definition of a successful refinement.) However, refinement would sometimes
get into a loop in which there would be a few successful refinements,
followed by one or more that would ``undo'' the improvements of the previous
ones.
For example, the largest 1-step error may cycle as
.
In general, cases were seen in which the number of refinements in these
loops was 3, 4, and up to about 8. Clearly a simple ``die when K successive
failures are seen'' is not general enough to catch this kind of loop.
Queuing theory provides a formula that is useful here. It defines an arithmetic running average A to be
where 
is the newest element added to the set, and is
the memory constant. The higher the memory constant, the longer
the memory -- i.e., the less the effect of an individual new element.
A rule of thumb is that A is roughly an average of the most recent
elements. Equation 2.0, however, is not suited for
measuring errors such as those in refinement
that can change by many orders of magnitude,
and is especially unsuited when smaller means better.
For example, a string of errors of followed by an
error of would average to about , whereas a change from
to is an indication that refinement is succeeding.
We thus need a geometric equivalent of equation 2.0, to allow values differing by orders of magnitude to average meaningfully.
I define the
geometric running average G as
where is the new element, and n is an integer,
, so higher n implies longer memory.
Both equations 2.0 and 2.1 require
initialization to some reasonable starting value 
and 
,
respectively. n should not be too large; I found 2 or 3 worked
best.
Finally, we want an equation that measures the improvement that is being made by successive refinements, rather than one that measures absolute error, because it is the change in 1-step errors that indicates whether current refinements are succeeding, not their absolute size. Note that the 1-step errors may stop decreasing for two reasons: (1) 1-step errors have reached the machine precision, or (2) refinement is failing to find a shadow. Using the improvement rather than the absolute value allows us to use the same algorithm to halt refinement in either case. Thus define the improvement I to be
If I is close to or greater than 1, then the current refinement did not improve on the previous one; if I << 1 then the current refinement is successful.
We have two refinement methods. In order of decreasing cost, they are recomputed RUS, and constant RUS. The general idea is: if refinement is working well with an expensive method, then switch to a cheaper one; if a cheaper one seems to be failing, switch to a more expensive one. If the most expensive one is failing, then give up refinement entirely, and return failure. Here is the heuristic I have built over many months of trial and error.
Further research in recomputed RUS could focus on whether there exists a
criterion to decide that a particular RUS needs recomputing, rather
than all of them. If this is the case, it could be an O(S) speed savings.
Also, there may be a place for SLES or other noise-reduction
procedures in the loop of expensive and cheap refinement algorithms (which
currently contains only the two above: recomputed RUS and constant RUS).
Finally, I note in passing that Newton's method is sometimes used with dampening when it is known that the correction factors may not be accurate, but are assumed to point roughly in the correct direction. In other words, equation 1.10 is modified to
for some constant 
. I briefly tried this
with the correction co-efficients 
,
but it did not seem to work. However, this result should not be taken as
conclusive, as I did not spend much time testing damped correction or trying
to make it work.
This idea is based on the same observation as constant RUS, and is only useful if constant RUS is employed. It takes advantage of the RUS for a noisy orbit B being near to the RUS for a nearby noisy orbit A. In particular, the shadows for two overlapping segments of a noisy orbit will be near to each other along the segment that the noisy segments overlap, and thus the RUS's for the overlapping segment will also be near each other. So, when trying to find a shadow for a segment B which is an extension to segment A, the RUS of A can be re-used on the segment of B that overlaps A.
One interesting question is whether to use the first or last RUS that
was computed for A, if A ever had to recompute the RUS. An argument
in favour of using the first is that the noisy orbit is exactly the
same, since B is just an extension of A. However, if A had to
recompute the RUS, then probably so will B if A's first RUS
is used. Recall that the RUS needed for the early refinements need not
be as accurate as the ones used later. Furthermore, we assume that the segment
of B's shadow that overlaps A's shadow will be closer to
A's shadow than the first few iterations of B is to the
first few iterations of A.
Thus, if we use the last RUS that A used, we are less likely to
recompute the RUS for B. If B is a subset of
A rather than an extension, then obviously no new RUS 's need be
computed. All shadowing runs in this thesis use the last RUS.
Finally, re-using the RUS allows a more fine-tuned search for where a glitch occurs, because it is much less expensive to attempt shadowing particular subsets of a noisy orbit once the entire RUS is computed.
A numerical solution of an ODE is represented by an ordered, discrete
sequence of points. Say we were to construct a continuous solution p(t)
from these points, for example by
using a suitably smooth and accurate interpolation. Then we could extend
the definition of 
shadowing for some true solution x(t)
by saying: x(t) -shadows p(t) on 
if
.
Now, it should be clear that we can choose any representative sequence of points along p(t) to use in the refinement algorithm introduced in the previous chapter; we need not choose the points from which p(t) was originally constructed. In particular, we can choose a subset of the original set of points, as long as enough points are chosen to be ``representative'' of p(t). The steps that are finally chosen are called shadow steps.
There are at least two reasons to desire as few shadow steps as possible:
First, if constant RUS is being used, then the RUS needs to be stored
in memory. Each RUS requires a matrix (the resolvent),
and two sets of basis vectors. Clearly the fewer shadow steps,
the less memory is required to store the RUS.
Second, if the ``accurate'' integrator has a large startup cost,
then the fewer startups that are required, the better. For example,
the Adams's methods I used take extremely small internal timesteps early
in the integration. Thus, for each shadow step, the Adams's method
must restart with extremely small stepsizes.
For the N-body simulations reported in this thesis, a set of ``standardized'' units was used [14] such that the scale of the system in all units of interest was of order 1 -- i.e., the system had a diameter of order 1, the crossing time was of order 1, and the N particles each had mass 1/N. In such a system, the timesteps of QT's integrator averaged about 0.01, and they used each timestep as a shadow step. I have found empirically that, in this system, using shadow steps of size 0.1 works well. Smaller shadow steps use more time and memory but could not find shadows any better. Shadow steps of 0.2 were slightly less reliable, and steps of size 0.5 were unreliable.
The important criterion for choosing shadow step sizes seems to be
the validity of the linear map. Recall that the linear map or
resolvent is a
first-order approximation that maps small perturbations of the
orbit p(t) from time to , so that a system
starting at 
evolves, to first order in 
,
to 
.
For this equation to be valid, must be small.
Since the computation
of the correction co-efficients in the GHYS refinement procedure depends
on this linear perturbation approximation,
the 1-step errors of our shadow steps must be
sufficiently small for the linear map to be valid. The larger the shadow
steps, the further the accurate solution will diverge from the noisy
solution, and thus the larger the correction needed per shadow step.
Although the allowable perturbation size is problem-dependent,
I have found empirically that, for the unit-sized N-body system used
here, perturbations of size 
are always small enough, while
perturbations of size about 
or greater start to show significant
difficulties. In general, however, a shadow step must be small enough
that the 1-step errors are small enough that
the linearized map is accurate enough that, when the correction is
applied at step i, the linearized map correctly maps the error
towards being smaller. In other words, if 
is the 1-step error
at 
, 
is the correction, 
is the linear map and 
is the exact perturbation map, then 
must be close to
in comparison to the size of the 1-step errors:
In practice, it is probably too difficult to use equation 2.2, and it may be necessary to experiment to find the largest allowable 1-step error, which then must be used to constrain the size of the shadow steps.
If the Lyapunov exponent 
of the system is known a priori, it may
be possible to choose shadow step sizes a priori. Note that
the divergence of the noisy and accurate orbits will be dominated by
the errors in the noisy orbit.
Say the noisy orbit has stepsizes of negligible length,
each with error 
.
Then each error will be magnified after a time T to 
.
If E is the maximum allowable 1-step error for which the linear map
is valid, then shadow steps should be no larger than
For our N-body systems, this equation gives an upper bound of about 1 to 10 time units, which is larger than the 0.1 sized shadow steps I used. Thus, the above equation seems a weak upper bound.
Even a system with a particular Lyapunov exponent may have short
intervals during which the local divergence rate is faster or
slower than the Lyapunov exponent would suggest. Thus, it may
be helpful to devise an algorithm that dynamically builds shadow steps.
One such algorithm, as yet untested, is as follows.
Assume that the timesteps in the noisy orbit are small in comparison
to the shadow steps that will be built.
Let the noisy orbit be 
at times 
.
Let E be the largest allowable 1-step error for which the linear map is
valid.
To construct a shadow step starting at time 
,
the accurate solution p(t) is initialized to
the noisy point 
.
Accurate integration of p(t) proceeds successively
to times 
until 
, when
marks the end of the shadow step.
The accurate solution is then re-initialized to 
to begin the
next shadow step.
Now, the first refinement is likely to have the largest 1-step errors; thus, the first refinement will need the smallest shadow steps, and thus the largest RUS set of any refinement. This means that a large RUS set needs to be computed at least once, but only to low accuracy (see the section on ``cheaper accurate integrator'').
Originally I thought that, as refinement proceeds to decrease the 1-step
errors, it would be
advantageous to construct larger-and-larger shadow steps.
However, I no longer believe this will
give much of a speed savings, because (1) If refinement is working well,
then constant RUS will be invoked, in which case there is no need to
recompute the RUS at all; (2) Conversely, if refinement is failing,
then there is no justification to increase the size of shadow steps -- in
fact, it may be advantageous to decrease them. Note that
if refinement is succeeding, it may be advantageous to use
larger-and-larger
shadow steps in the computation of the 1-step errors, even though
the RUS is not being recomputed.
Finally, implementing dynamic shadow step sizes may help in another area. As described above, I currently discard all progress made by constant RUS if it begins to fail, reverting to the orbit and RUS of the most recent refinement that computed the RUS. However, if constant RUS works for several refinements but then starts to fail, perhaps it would be advantageous to use the orbit of the most recent successful refinement to build new shadow steps using the above dynamic algorithm, regardless of whether the most recent successful refinement computed the RUS or not.
When computing the 1-step errors of a noisy orbit, we must
use an integrator that has smaller 1-step errors than the
integrator used to compute the noisy orbit. The question is,
how much more accurate does it need to be? During early
refinements when the 1-step errors are large, the errors in
the correction factors may be dominated by the first-order
approximation of the resolvents, so the 1-step errors need not
be computed to machine precision. In practice, I have found that
it is sufficient to compute the 1-step errors to an accuracy
that of the size of the maximum 1-step error of the previous
refinement; computing them any more accurately does not speed refinement,
although computing them only 
more accurately
sometimes results in more iterations of the refinement procedure.
In addition, a factor of only is not enough because
some integrators have sufficiently gross control of their errors
that requesting only 2 extra digits will result in the integrator
returning exactly the same result.
Note it is necessary to loosen this criterion when the 1-step errors
are within of the machine precision, in order not to
request more accuracy than the machine precision allows.
The accuracy required to compute the resolvents is less clear. So far, when reverting to recomputed RUS, I have been computing them to the same accuracy as the 1-step errors, described in the previous paragraph. This may be more precision than is necessary, if, for example, the resolvents change more quickly owing to movement of the orbit than to errors in their construction. In other words, it may be sufficient to always compute a resolvent to some constant precision, and only recompute it if the numerical shadow drifts sufficiently far from the original noisy orbit that the resolvent no longer correctly maps small perturbations from one shadow step to the next.
The only methods I have tried as my accurate integrator are Adams's methods. It may be wise to try others. In particular, if the shadow steps are small, it may pay to use a less sophisticated routine, such as a high-order explicit Runge-Kutta method. If the shadow steps are large, an Adams's or a Bulirsch-Stoer method is probably apt, because even though they both have high startup cost, they can eventually move quickly along the solution if they are not forced to restart too often. It may also be interesting to attempt using extended precision integration to test the accuracy of the standard (double precision) routines.
Finally, an important factor in problems, like the N-body problem, that have a large variance of scales all occuring at once (i.e., some pairs of stars are several orders of magnitude closer to each other than other pairs) is a concept called individual time steps. The modern hand-coded N-body integrator gives each star a personalized integration timestep; stars that have high accelerations are integrated with smaller timesteps than those with lower accelerations. Perhaps it would be fruitful to attempt to write a general-purpose integration routine that uses individual timesteps for each dimension. However, such an integrator is beyond the scope of this thesis.
To quantify the speedup of the optimizations, 32 noisy orbits
were chosen, and each was shadowed using several different combinations of the
optimizations. In each case, the system consisted of 99 fixed particles
and one moving particle (i.e., N=100,M=1),
identical to the shadowing experiments of QT.
Forces were not softened.
The 32 orbits were chosen by generating random 3-dimensional positions for
all particles from the uniform distribution on (0,1);
a 3-dimensional random initial velocity for the moving particle was
also chosen uniformly on (0,1).
The standardized units of Heggie and Mathieu
[14] were used, in which each particle has mass 1/N.
The pseudo-random number generator was the popular 48-bit drand48(),
with seeds 1 through 32. The seed 1 case was run on a Sun SPARCstation
10/514 with a 50 MHz clock; seed cases 2 through 32 were run on 25 MHz
Sun SPARCstation IPC's (each about 1/8 the speed of the SS10/514).
Once the initial conditions were set, each noisy orbit was generated
by integrating for 1.28 standard time units (about 1 crossing time)
using LSODE [16] with pure relative error control of .
This figure agreed well with the magnitude of the initial 1-step errors
computed during refinement.
Although one crossing time sounds short, it is long enough that 5 of
the orbits contained trouble spots.
Furthermore, the number of unoptimized QT refinements required to find a shadow that
has no trouble spots seems independent of the length of the orbit --
each refinement takes much longer, but the convergence is still
geometric per refinement. Thus, the results below should be independent
of the length of the orbit, as long as the length is non-trivial.
This is what has been observed with the
longer orbits I have shadowed, although I do not document them here.
For short shadow steps, a constant shadow step size of 0.01 was used, which approximates the average sized shadow step in QT. This results in 128 shadow steps. For large shadow steps, 16 shadow steps of size 0.08 were used. As in a usual shadowing attempt, longer and longer segments are shadowed in an attempt to find the longest shadow. Here, each successive segment had twice as many shadow steps as the previous one, up to 16 and 128, for long and short shadow steps, respectively. No attempt was made to isolate glitches more accurately than this factor of two.
The highest tolerance requested of the accurate integrator was 
.
A successful numerical shadow was defined to be one whose 1-step errors
were all less than 
. This number was chosen simply
because it was the smallest number that geometrically converging
refinement sequences could consistently achieve;
was too small,
because many refinement sequences would proceed geometrically
until their maximum 1-step error was about 
,
and then they would ``bounce around''
for many refinements until, apparently by chance, the maximum 1-step error would
fall below .
The maximum allowed shadow distance was 0.1, although none over 0.0066 were observed with successful shadows.
The following speedup table displays the speedups of the various optimizations. All ratios are speedup factors with respect to the time column.
| time(s): | time in seconds for unoptimize version. |
| QT: | original code of Quinlan & Tremaine |
| L: | L arge shadow steps |
| I: | backward resolvent by Inverting forward resolvent |
| C: | Cheaper accurate integrator |
| R: | constant RUS |
| U: | re-Use RUS from previous successful shadow (appears only in combinations) |
| seed | time(s) | QT | L | I | C | R | CR | CUR | CLR | CULR | CULRI |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1442 | 1.06 | 4.54 | 2.01 | 1.96 | 3.00 | 8.87 | 14.2 | 30.8 | 37.2 | 47.4 |
| 2 | 9379 | 0.707 | 6.08 | 1.82 | 3.09 | 3.48 | 11.2 | 15.7 | 52.3 | 68.3 | 75.7 |
| 3 | 7847 | 0.728 | 6.30 | 1.88 | 2.36 | 2.56 | 9.29 | 13.0 | 44.0 | 59.7 | 65.5 |
| 4 | 7011 | 0.866 | 11.1 | 1.98 | 2.74 | 2.84 | 7.88 | 12.3 | 40.5 | 55.8 | 74.3 |
| 5 | 12204 | 0.933 | 12.2 | 2.13 | 2.42 | 1.08 | 1.66 | 1.54 | 5.31 | 4.96 | 8.0 |
| 6 | 9443 | 1.14 | 7.24 | 2.01 | 3.18 | 3.98 | 10.8 | 13.5 | 5.36 | 56.8 | 29.8 |
| 7 | 6277 | 1.13 | 5.51 | 1.85 | 2.63 | 2.71 | 8.50 | 11.6 | 46.9 | 63.7 | 82.9 |
| 8 | 6582 | 1.13 | 4.79 | 2.04 | 1.91 | 2.79 | 7.09 | 10.6 | 33.8 | 45.4 | 56.9 |
| 9 | 7154 | 1.14 | 4.33 | 1.92 | 1.96 | 2.70 | 7.74 | 11.5 | 30.5 | 39.6 | 51.9 |
| 10 | 5832 | 1.13 | 4.32 | 1.87 | 1.54 | 2.72 | 6.46 | 10.7 | 29.1 | 45.5 | 57.2 |
| 11 | 6659 | 1.13 | 5.10 | 1.93 | 2.34 | 2.65 | 7.40 | 10.7 | 37.1 | 50.7 | 62.9 |
| 12 | 8623 | 0.861 | 5.00 | 2.44 | 2.57 | 3.37 | 9.64 | 13.7 | 44.8 | 52.4 | 75.4 |
| 13 | 14566 | 0.452 | 4.34 | 1.00 | 4.52 | 0.784 | 0.931 | 0.939 | 5.67 | 5.15 | 7.6 |
| 14 | 6976 | 0.749 | 4.54 | 2.00 | 2.17 | 2.85 | 7.23 | 11.1 | 32.9 | 45.2 | 49.4 |
| 15 | 5664 | 0.729 | 4.79 | 2.02 | 1.89 | 2.71 | 6.83 | 10.2 | 33.5 | 45.4 | 62.9 |
| 16 | 6634 | 1.15 | 4.89 | 1.97 | 1.82 | 2.64 | 7.35 | 10.6 | 33.8 | 44.8 | 58.7 |
| 17 | 6854 | 0.946 | 4.96 | 2.06 | 2.16 | 2.88 | 8.97 | 12.7 | 47.2 | 60.8 | 83.2 |
| 18 | 4932 | 0.629 | 2.88 | 1.74 | 1.69 | 2.17 | 5.38 | 7.84 | 25.7 | 34.1 | 45.7 |
| 19 | 8470 | 1.06 | 5.16 | 2.98 | 2.96 | 1.32 | 4.37 | 4.02 | 31.1 | 27.5 | 53.5 |
| 20 | 4566 | 1.12 | 5.59 | 1.91 | 2.04 | 2.78 | 6.21 | 9.50 | 33.7 | 48.6 | 64.3 |
| 21 | 7409 | 1.07 | 6.01 | 2.00 | 2.92 | 2.86 | 9.59 | 13.4 | 46.6 | 61.3 | 82.2 |
| 22 | 6988 | 1.22 | 4.89 | 2.17 | 2.00 | 3.03 | 7.34 | 11.4 | 36.1 | 44.0 | 57.2 |
| 23 | 7699 | 0.750 | 4.66 | 1.93 | 1.91 | 3.20 | 8.27 | 10.4 | 35.2 | 46.3 | 51.1 |
| 24 | 8851 | 1.18 | 2.53 | 1.79 | 2.78 | 2.89 | 10.2 | 15.4 | 52.9 | 71.1 | 93.1 |
| 25 | 7287 | 1.13 | 3.58 | 1.96 | 2.67 | 2.53 | 7.58 | 11.5 | 34.1 | 47.4 | 59.3 |
| 26 | 10736 | 0.854 | 7.74 | 2.84 | 2.79 | 4.33 | 12.4 | 16.9 | 58.2 | 76.5 | 81.1 |
| 27 | 7001 | 1.13 | 5.07 | 2.01 | 2.24 | 2.79 | 8.35 | 12.1 | 38.9 | 54.5 | 70.1 |
| 28 | 7324 | 1.13 | 4.49 | 2.06 | 1.93 | 2.72 | 8.01 | 11.2 | 33.2 | 49.3 | 55.0 |
| 29 | 13779 | 0.802 | 4.01 | 1.89 | 2.01 | 0.898 | 1.16 | 1.15 | 4.03 | 3.99 | 6.5 |
| 30 | 7932 | 1.14 | 10.9 | 2.01 | 2.17 | 2.81 | 8.82 | 13.0 | 43.3 | 67.5 | 86.7 |
| 31 | 6989 | 1.20 | 5.57 | 2.26 | 2.37 | 2.81 | 8.44 | 12.3 | 47.4 | 57.2 | 77.6 |
| 32 | 6720 | 1.08 | 4.80 | 1.89 | 1.90 | 2.78 | 7.61 | 11.5 | 34.0 | 50.5 | 65.5 |
| avg | 7682 | 1.07 | 5.56 | 2.01 | 2.36 | 2.68 | 7.55 | 10.8 | 34.6 | 47.5 | 59.3 |
[Note (30 Dec 1996): a more recent technical report has added still more optimizations].
There are several interesting observations to make about this table. First, note that the run times of the original QT algorithm are comparable to the run times of my unoptimized version (differing on average by a factor of 1.07), as would be expected. Now looking at each optimization acting alone, we see that using Large Shadow Steps 8 times longer than QT (column L) gives an average speedup of about 5.5. The large shadow steps implemented here (every 8 small shadow steps) was trivial to implement, so I would recommend that, even if no other optimizations are used, large shadow steps are worthwhile. Third, inverting the forward resolvent to produce the inverse resolvent (column I) produces the expected average speedup of 2.0. Fourth, the cheap accurate integrator (column C) gives an average speedup of 2.36. This is about what is expected, because both the QT and C algorithms on average require just over 3 refinements to converge, and all C refinements are cheaper than a QT refinement except the last one, which is about equal in expense. Finally, using constant RUS gives a speedup of almost 3. Again this is about what is expected because QT requires about 3 refinements to converge while R has one RUS computation followed by several cheap constant RUS refinements.
Next we look at combinations of optimizations. First, it is interesting
to note that combining the cheap accurate integrator C with
constant RUS R results in an average speedup that is greater than the product of
the two individual speedups ( 
). This
is because, when using CR, only one RUS is computed,
and it is computed cheaply. Using R alone requires
computing the one RUS to high accuracy; using C alone requires computing
at least one RUS (the final one) to high accuracy. Second, re-Using
the RUS of a previous successful shadow
(U or re-Use RUS, seen in column CUR)
makes sense only when R is also used. It gives a speedup
of about 43% over CR. This is less than a factor of 2 because, with
C, the resolvents are computed sufficiently cheaply that the time to
do a constant RUS iteration is becoming non-negligible. Presumably
if a UR column existed, it would show a speedup over the R column
closer to 2. The last three columns show other combinations.
The most important point to note is that, except for CR, the combinations
give a speedup less than the product of any appropriate choice of previous
columns. Perhaps this is at least partially owing to an affect similar
to Ahmdal's Law: there still
exist parts of the algorithm that have not been sped up, and as the
remainder of the program that is being optimized speeds up, these
unoptimized sections take a greater proportion of the time.
Finally, it will be noticed that orbits 5, 6, 13, 19, and 29 obtained
speedups significantly smaller than average in some columns. These
are the orbits that either contained glitches or trouble spots. I will deal with these on
a case-by-case basis, since there are several interesting points to be made.
Errata InsertionThe corrected energy fluctuations are more jagged than in the original diagrams, although much smaller in magnitude (at least 4 orders of magnitude smaller!).
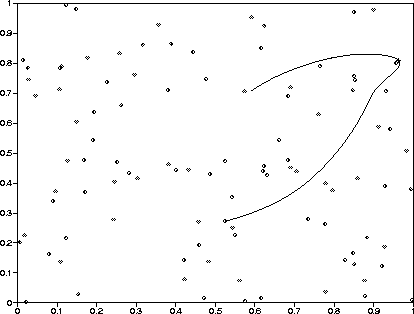
Figure 2.1: Orbit 5 projected onto the xy plane. The close encounter is
near the right-most extent of the orbit. The ``+'' marks the point in
the orbit where the 1-step errors could not be decreased below ,
and corresponds to the timestep of closest approach. The particle attached
to the bottom end of the orbit near (0.52,0.27) is the moving particle at
its initial position.
The energy of the real system should be exactly constant. The energy of the simulations is conserved to about 6 digits, so for the energy plots, a constant of about 6 digits was subtracted from the energy to more clearly show the fluctuations.
Figure 2.2 shows that the energy of orbit 5 plunged dramatically at step 83.
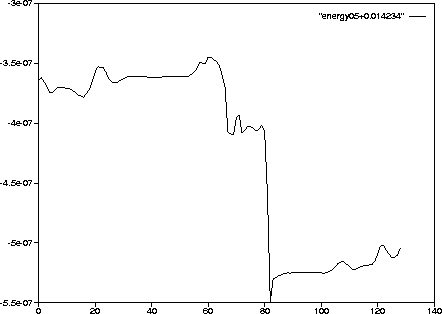
Figure 2.2: The [errata corrected] total energy (kinetic + gravitational potential,
shifted +0.014234)
of orbit 5 (unshadowable).
The sharp decline at timestep 83 marks the close approach
that caused the trouble spot. The drop is about 
,
and the total energy fluctuation is about 
, or about
.
The orbit could be shadowed for its first half, but
not over its entire length, because it contained a trouble
spot at the close encounter, where the 1-step error could not be
decreased below about .
This orbit obtained the greatest
speedup when the only active optimization was L -- the final 3 columns
show that the algorithm was slower when other optimizations were
added. The reason seems to be constant RUS: since the 1-step errors could
be reduced reliably down to , but no lower, the algorithm switched
many times to constant RUS (at which point the 1-step errors would be
decreased to , but no lower), and then back to recomputed RUS,
which would run for 1 or 2 refinements, producing refinements better than
constant RUS but not geometric; then the algorithm would switch back to
constant RUS, again decreasing the 1-step errors to , then switch
back to recomputed RUS, and so forth.
Since all progress of a sequence of constant
RUS refinements is discarded, progress was slow, until, finally,
recomputed RUS refinements got down to , at which point the
algorithm conceded defeat. However, other columns still make sense:
for example, comparing column CULR to CULRI shows a speedup of
almost 2, which is expected with the I optimization.
The refinement algorithm came excruciatingly close
to finding a numerical shadow for this orbit,
at one point achieving a maximum 1-step error of 
at timestep 87.
Columns L, C, R, and CR show significant speedups, but the
combination CLR has an large drop in speedup, suffering the same
alternation between constant RUS and recomputed RUS as did orbit 5.
Perhaps the Large Shadow Step at that point was just slightly too large,
thus having a linear map that was invalid. A similar fate
befell the column CULRI, which is surprising considering that only
half as many resolvents as column CULR were computed per
recomputed RUS refinement.
Shadowing
was easily successful for all attempts that only included the first
half of the orbit. However, the
attempt to shadow the entire orbit was fraught with problems trying to
satisfy the extreme sensitivity of the orbit to two close encounters.
The second encounter was sufficiently close that the LSODE
integrator in the non-optimized version suffered a fatal convergence error
on the 4th refinement, trying to integrate the backwards
resolvent past the encounter.
This explains why the I column shows no speedup:
it did not integrate any resolvents backwards, and by chance the forward
resolvents could be integrated well enough that it tried more than twice
as many refinement iterations than the unoptimized version before giving
up.
The R version took longer because of time spent alternating between constant
and recomputed RUS.
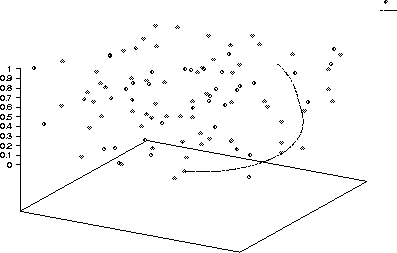
Figure 2.3: Orbit 19. Note there are no close encounters. It is not clear
why this orbit was not shadowable.
The energy fluctuations (Figure 2.4) are about 1/3 of those of orbit 5, although they are just as jagged.
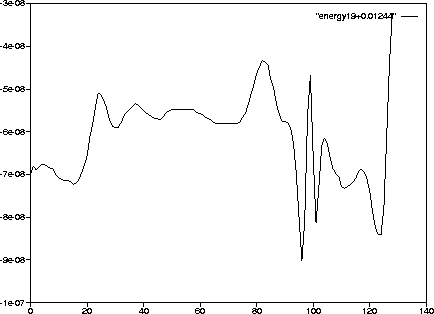
Figure 2.4: [Errata corrected] energy of orbit 19, shifted +0.01244 (unshadowable).
The first jagged drop in the energy curve near timestep 96 is about 
, while the total fluctuation is about 
, about 1/3 that of orbit 5.
Figure 2.5 shows the energy of orbit 22, that was shadowable. Furthermore, I looked at all 32 energy figures and almost all of them had fluctuations similar to the ones shown here, even though most of the 32 orbits were shadowable over the 1.28 time interval used. Thus it seems that energy fluctuations may not, in themselves, be enough to detect non-shadowability.
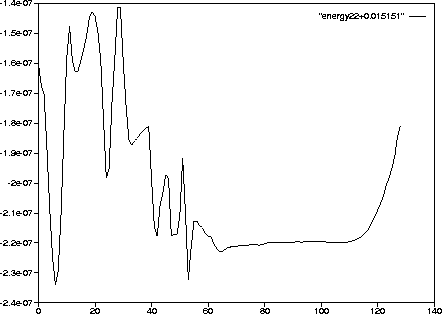
Figure 2.5: Corrected energy of orbit 22, shifted by 0.015151.
This orbit was shadowable.
The fluctuations near the beginning of the orbit are about
. The energy fluctuations are slightly
bigger (percentage-wise) than orbit 19, and just as jagged. Thus,
it seems energy fluctuations alone cannot explain why this orbit
was shadowable while 5 and 19 were not.
The largest 1-step errors were consistently at or near time 0. Since the entire orbit appeared extremely smooth, it is not understood why no shadow could be found over the entire length of the noisy orbit.
Finally, referring to the speedup table, most of the speedups appear reasonable.
There are many other observations about the shadowing attempts that cannot be seen in the table.
time, and computing a 1-step error takes only 
time, this
speedup is asymptotically O(M). 
